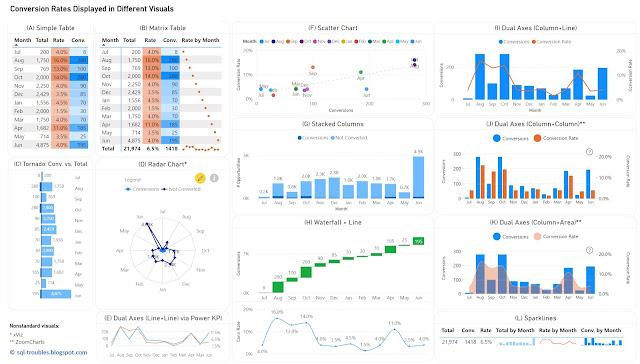
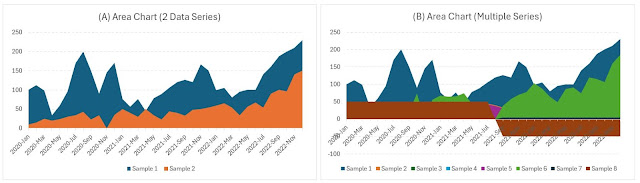
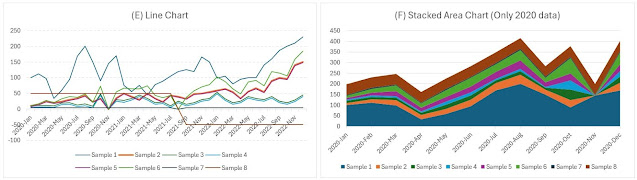
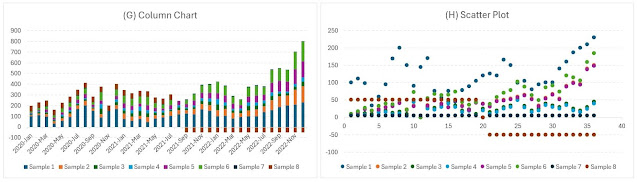
"If statistical graphics, although born just yesterday, extends its reach every day, it is because it replaces long tables of numbers and it allows one not only to embrace at glance the series of phenomena, but also to signal the correspondences or anomalies, to find the causes, to identify the laws." (Émile Cheysson, cca. 1877)
"In any chart where index numbers are used the greatest care should be taken to select as unity a set of conditions thoroughly typical and representative. It is frequently best to take as unity the average of a series of years immediately preceding the years for which a study is to be made. The series of years averaged to represent unity should, if possible, be so selected that they will include one full cycle or wave of fluctuation. If one complete cycle involves too many years, the years selected as unity should be taken in equal number on either side of a year which represents most nearly the normal condition." (Willard C Brinton, "Graphic Methods for Presenting Facts", 1919)
"A graph is a pictorial representation or statement of a series of values all drawn to scale. It gives a mental picture of the results of statistical examination in one case while in another it enables calculations to be made by drawing straight lines or it indicates a change in quantity together with the rate of that change. A graph then is a picture representing some happenings and so designed as to bring out all points of significance in connection with those happenings. When the curve has been plotted delineating these happenings a general inspection of it shows the essential character of the table or formula from which it was derived." (William C Marshall, "Graphical methods for schools, colleges, statisticians, engineers and executives", 1921)
"A series ot quantities or values can be most simply and often best shown by a series of corresponding lines or bars. All bars being drawn against one and the same scale, their lengths vary with the amounts which they represent." (Karl G Karsten, "Charts and Graphs", 1925)
"Although, the tabular arrangement is the fundamental form for presenting a statistical series, a graphic representation - in a chart or diagram - is often of great aid in the study and reporting of statistical facts. Moreover, sometimes statistical data must be taken, in their sources, from graphic rather than tabular records." (William L Crum et al, "Introduction to Economic Statistics", 1938)
"[….] double-scale charts are likely to be misleading unless the two zero values coincide" (either on or off the chart). To insure an accurate comparison of growth the scale intervals should be so chosen that both curves meet at some point. This treatment produces the effect of percentage relatives or simple index numbers with the point of juncture serving as the base point. The principal advantage of this form of presentation is that it is a short-cut method of comparing the relative change of two or more series without computation. It is especially useful for bringing together series that either vary widely in magnitude or are measured in different units and hence cannot be compared conveniently on a chart having only one absolute-amount scale. In general, the double scale treatment should not be used for presenting growth comparisons to the general reader." (Kenneth W Haemer, "Double Scales Are Dangerous", The American Statistician Vol. 2" (3) , 1948)
"If a chart contains a number of series which vary widely in individual magnitude, optical distortion may result from the necessarily sharp changes in the angle of the curves. The space between steeply rising or falling curves always appears narrower than the vertical distance between the plotting points." (Rufus R Lutz, "Graphic Presentation Simplified", 1949)
"The use of two or more amount scales for comparisons of series in which the units are unlike and, therefore, not comparable [...] generally results in an ineffective and confusing presentation which is difficult to understand and to interpret. Comparisons of this nature can be much more clearly shown by reducing the components to a comparable basis as percentages or index numbers." (Rufus R Lutz, "Graphic Presentation Simplified", 1949)
"First, it is generally inadvisable to attempt to portray a series of more than four or five categories by means of pie charts. If, for example, there are six, eight, or more categories, it may be very confusing to differentiate the relative values portrayed, especially if several small sectors are of approximately the same size. Second, the pie chart may lose its effectiveness if an attempt is made to compare the component values of several circles, as might be found in a temporal or geographical series. In such case the one-hundred percent bar or column chart is more appropriate. Third, although the proportionate values portrayed in a pie chart are measured as distances along arcs about the circle, actually there is a tendency to estimate values in terms of areas of sectors or by the size of subtended angles at the center of the circle." (Calvin F Schmid, "Handbook of Graphic Presentation", 1954)
"Where the values of a series are such that a large part the grid would be superfluous, it is the practice to break the grid thus eliminating the unused portion of the scale, but at the same time indicating the zero line. Failure to include zero in the vertical scale is a very common omission which distorts the data and gives an erroneous visual impression." (Calvin F Schmid, "Handbook of Graphic Presentation", 1954)
"Besides being easier to construct than a bar chart, the line chart possesses other advantages. It is easier to read, for while the bars stand out more prominently than the line, they tend to become confusing if numerous, and especially so when they record alternate increase and decrease. It is easier for the eye to follow a line across the face of the chart than to jump from bar top to bar top, and the slope of the line connecting two points is a great aid in detecting minor changes. The line is also more suggestive of movement than arc bars, and movement is the very essence of a time series. Again, a line chart permits showing two or more related variables on the same chart, or the same variable over two or more corresponding periods." (Walter E Weld, "How to Chart; Facts from Figures with Graphs", 1959)
"Pie charts have weaknesses and dangers inherent in their design and application. First, it is generally inadvisable to attempt to portray more than four or five categories in a circle chart, especially if several small sectors are of approximately the same size. It may be very confusing to differentiate the relative values. Secondly, the pie chart loses effectiveness if an effort is made to compare the component values of several circles, as might occur in a temporal or geographical series. [...] Thirdly, although values are measured by distances along the arc of the circle, there is a tendency to estimate values in terms of areas by size of angle. The 100-percent bar chart is often preferable to the circle chart's angle and area comparison as it is easier to divide into parts, more convenient to use, has sections that may be shaded for contrast with grouping possible by bracketing, and has an easily readable percentage scale outside the bars." (Anna C Rogers, "Graphic Charts Handbook", 1961)
"Since bars represent magnitude by their length, the zero line must be shown and the arithmetic scale must not be broken. Occasionally an excessively long bar in a series of bars may be broken off at the end, and the amount involved shown directly beyond it, without distorting the general trend of the other bars, but this practice applies solely when only one bar exceeds the scale." (Anna C Rogers, "Graphic Charts Handbook", 1961)
"The impression created by a chart depends to a great extent on the shape of the grid and the distribution of time and amount scales. When your individual figures are a part of a series make sure your own will harmonize with the other illustrations in spacing of grid rulings, lettering, intensity of lines, and planned to take the same reduction by following the general style of the presentation." (Anna C Rogers, "Graphic Charts Handbook", 1961)
"An especially effective device for enhancing the explanatory power of time-series displays is to add spatial dimensions to the design of the graphic, so that the data are moving over space" (in two or three dimensions) as well as over time. […] Occasionally graphics are belligerently multivariate, advertising the technique rather than the data." (Edward R Tufte, "The Visual Display of Quantitative Information", 1983)
"The bar graph and the column graph are popular because they are simple and easy to read. These are the most versatile of the graph forms. They can be used to display time series, to display the relationship between two items, to make a comparison among several items, and to make a comparison between parts and the whole" (total). They do not appear to be as 'statistical', which is an advantage to those people who have negative attitudes toward statistics. The column graph shows values over time, and the bar graph shows values at a point in time. bar graph compares different items as of a specific time" (not over time)." (Anker V Andersen, "Graphing Financial Information: How accountants can use graphs to communicate", 1983)
"The time-series plot is the most frequently used form of graphic design. With one dimension marching along to the regular rhythm of seconds, minutes, hours, days, weeks, months, years, centuries, or millennia, the natural ordering of the time scale gives this design a strength and efficiency of interpretation found in no other graphic arrangement." (Edward R Tufte, "The Visual Display of Quantitative Information", 1983)
"There are several uses for which the line graph is particularly relevant. One is for a series of data covering a long period of time. Another is for comparing several series on the same graph. A third is for emphasizing the movement of data rather than the amount of the data. It also can be used with two scales on the vertical axis, one on the right and another on the left, allowing different series to use different scales, and it can be used to present trends and forecasts." (Anker V Andersen, "Graphing Financial Information: How accountants can use graphs to communicate", 1983)
"A connected graph is appropriate when the time series is smooth, so that perceiving individual values is not important. A vertical line graph is appropriate when it is important to see individual values, when we need to see short-term fluctuations, and when the time series has a large number of values; the use of vertical lines allows us to pack the series tightly along the horizontal axis. The vertical line graph, however, usually works best when the vertical lines emanate from a horizontal line through the center of the data and when there are no long-term trends in the data." (William S Cleveland, "The Elements of Graphing Data", 1985)
"[decision trees are the] most picturesque of all the allegedly scientific aids to making decisions. The analyst charts all the possible outcomes of different options, and charts all the latters' outcomes, too. This produces a series of stems and branches" (hence the tree). Each of the chains of events is given a probability and a monetary value." (Robert Heller, "The Pocket Manager", 1987)
"Grouped area graphs sometimes cause confusion because the viewer cannot determine whether the areas for the data series extend down to the zero axis. […] Grouped area graphs can handle negative values somewhat better than stacked area graphs but they still have the problem of all or portions of data curves being hidden by the data series towards the front." (Robert L Harris, "Information Graphics: A Comprehensive Illustrated Reference", 1996)
"Time-series forecasting is essentially a form of extrapolation in that it involves fitting a model to a set of data and then using that model outside the range of data to which it has been fitted. Extrapolation is rightly regarded with disfavour in other statistical areas, such as regression analysis. However, when forecasting the future of a time series, extrapolation is unavoidable." (Chris Chatfield, "Time-Series Forecasting" 2nd Ed, 2000)
"Comparing series visually can be misleading […]. Local variation is hidden when scaling the trends. We first need to make the series stationary" (removing trend and/or seasonal components and/or differences in variability) and then compare changes over time. To do this, we log the series" (to equalize variability) and difference each of them by subtracting last year’s value from this year’s value." (Leland Wilkinson, "The Grammar of Graphics" 2nd Ed., 2005)
"In general. statistical graphics should be moderately greater in length than in height. And, as William Cleveland discovered, for judging slopes and velocities up and down the hills in time-series, best is an aspect ratio that yields hill - slopes averaging 45°, over every cycle in the time-series. Variations in slopes are best detected when the slopes are around 45°, uphill or downhill." (Edward R Tufte, "Beautiful Evidence", 2006)
"[...] if you want to show change through time, use a time-series chart; if you need to compare, use a bar chart; or to display correlation, use a scatter-plot - because some of these rules make good common sense." (Alberto Cairo, "The Functional Art", 2011)
"if you want to show change through time, use a time-series chart; if you need to compare, use a bar chart; or to display correlation, use a scatter-plot - because some of these rules make good common sense." (Alberto Cairo, "The Functional Art", 2011)
"Bubble charts are a type of area chart that use discrete or contin�uous data and can be used to display nominal and ranking relationships. You would seldom use them to show only a time series or part-to-whole relationship. Bubble charts can be used to compare subcategories’ values, in either side-by-side comparisons, or in more elaborate graph types such as bubble plots (when showing ranking and time series) and bubble maps (if geography was germane to the story being told). They are most valuable when the range of data set is large, and there is a good amount of variance between the smallest and the largest subcategories. They can also be use�ful when using bar charts simply looks awkward." (Jason Lankow et al, "Infographics: The power of visual storytelling", 2012)
"When using dot plots to show a time series relationship, the scale does not have to start at a zero baseline. For the other relationships they do, however. For a time series relationship, the scale can be truncated if there is a story worth telling in the data that would otherwise be obscured by using a very large scale. However, you should use discretion when attempting to do this; a good rule of thumb is to use a scale in which the range of the dot plots consists of two-thirds of the graph’s total height, in or�der to display data trends more clearly. Additionally, if your goal is to show a time series relationship with continual data, you can throw a line on it, connecting the points. Essentially, you can use a series of straight lines between the points, which will help guide the reader’s eyes from left to right." (Jason Lankow et al, "Infographics: The power of visual storytelling", 2012)
"The first myth is that prediction is always based on time-series extrapolation into the future (also known as forecasting). This is not the case: predictive analytics can be applied to generate any type of unknown data, including past and present. In addition, prediction can be applied to non-temporal" (time-based) use cases such as disease progression modeling, human relationship modeling, and sentiment analysis for medication adherence, etc. The second myth is that predictive analytics is a guarantor of what will happen in the future. This also is not the case: predictive analytics, due to the nature of the insights they create, are probabilistic and not deterministic. As a result, predictive analytics will not be able to ensure certainty of outcomes." (Prashant Natarajan et al, "Demystifying Big Data and Machine Learning for Healthcare", 2017)
"With time series though, there is absolutely no substitute for plotting. The pertinent pattern might end up being a sharp spike followed by a gentle taper down. Or, maybe there are weird plateaus. There could be noisy spikes that have to be filtered out. A good way to look at it is this: means and standard deviations are based on the naïve assumption that data follows pretty bell curves, but there is no corresponding 'default' assumption for time series data" (at least, not one that works well with any frequency), so you always have to look at the data to get a sense of what’s normal. [...] Along the lines of figuring out what patterns to expect, when you are exploring time series data, it is immensely useful to be able to zoom in and out." (Field Cady, "The Data Science Handbook", 2017)
"A time series is a sequence of values, usually taken in equally spaced intervals. […] Essentially, anything with a time dimension, measured in regular intervals, can be used for time series analysis." (Andy Kriebel & Eva Murray, "#MakeoverMonday: Improving How We Visualize and Analyze Data, One Chart at a Time", 2018)
"Heat maps are effective visualizations for seeing concentrations as well as patterns. Adding time series to a heat map can also reveal seasonality that may not be obvious otherwise." (Andy Kriebel & Eva Murray, "#MakeoverMonday: Improving How We Visualize and Analyze Data, One Chart at a Time", 2018)
"Many statistical procedures perform more effectively on data that are normally distributed, or at least are symmetric and not excessively kurtotic" (fat-tailed), and where the mean and variance are approximately constant. Observed time series frequently require some form of transformation before they exhibit these distributional properties, for in their 'raw' form they are often asymmetric." (Terence C Mills, "Applied Time Series Analysis: A practical guide to modeling and forecasting", 2019)
"Showing the data and reducing the clutter means reducing extraneous gridlines, markers, and shades that obscure the actual data. Active titles, better labels, and helpful annotations will integrate your chart with the text around it. When charts are dense with many data series, you can use color strategically to highlight series of interest or break one dense chart into multiple smaller versions. " (Jonathan Schwabish, "Better Data Visualizations: A guide for scholars, researchers, and wonks", 2021)