Data Science: Fractal (Definitions)

"A fractal is a mathematical set or concrete object that is irregular or fragmented at all scales [...]" (Benoît Mandelbrot, "The Fractal Geometry of Nature", 1982)

"Objects (in particular, figures) that have the same appearance when they are seen on fine and coarse scales." (David Rincón & Sebastià Sallent, Scaling Properties of Network Traffic, 2008) "A collection of objects that have a power-law dependence of number on size." (Donald L Turcotte, "Fractals in Geology and Geophysics", 2009) 

"A fractal is a geometric object which is self-similar and characterized by an effective dimension which is not an integer." (Leonard M Sander, "Fractal Growth Processes", 2009) 

"A fractal is a structure which can be subdivided into parts, where the shape of each part is similar to that of the original structure." (Yakov M Strelniker, "Fractals and Percolation", 2009) 

"A fractal is an image that comprises two distinct attributes: infinite detail and self-similarity." (Daniel C. Doolan et al, "Unlocking the Hidden Power of the Mobile", 2009)

"A geometrical object that is invariant at any scale of magnification or reduction." (Sidney Redner, "Fractal and Multifractal Scaling of Electrical Conduction in Random Resistor Networks", 2009) 

[Fractal structure:] "A pattern or arrangement of system elements that are self-similar at different spatial scales." (Michael Batty, "Cities as Complex Systems: Scaling, Interaction, Networks, Dynamics and Urban Morphologies", 2009) 

"A set whose (suitably defined) geometrical dimensionis non-integral. Typically, the set appears selfsimilar on all scales. A number of geometrical objects associated with chaos (e. g. strange attractors) are fractals." (Oded Regev, "Chaos and Complexity in Astrophysics", 2009) 

[Fractal system:] "A system characterized by a scaling law with a fractal, i. e., non-integer exponent. Fractal systems are self-similar, i. e., a magnification of a small part is statistically equivalent to the whole." (Jan W Kantelhardt, "Fractal and Multifractal Time Series", 2009) 

"An adjective or a noun representing complex configurations having scale-free characteristics or self-similar properties. Mathematically, any fractal can be characterized by a power law distribution." (Misako Takayasu & Hideki Takayasu, "Fractals and Economics", 2009) 

"Fractals are complex mathematical objects that are invariant with respect to dilations (self-similarity) and therefore do not possess a characteristic length scale. Fractal objects display scale-invariance properties that can either fluctuate from point to point (multifractal) or be homogeneous (monofractal). Mathematically, these properties should hold over all scales. However, in the real world, there are necessarily lower and upper bounds over which self-similarity applies." (Alain Arneodo et al, "Fractals and Wavelets: What Can We Learn on Transcription and Replication from Wavelet-Based Multifractal Analysis of DNA Sequences?", 2009) 

"Mathematical object usually having a geometrical representation and whose spatial dimension is not an integer. The relation between the size of the object and its “mass” does not obey that of usual geometrical objects." (Bastien Chopard, "Cellular Automata: Modeling of Physical Systems", 2009) 

 "A fragmented geometric shape that can be split up into secondary pieces, each of which is approximately a smaller replica of the whole, the phenomenon commonly known as self similarity." (Khondekar et al, "Soft Computing Based Statistical Time Series Analysis, Characterization of Chaos Theory, and Theory of Fractals", 2013) 

 "A natural phenomenon or a mathematical set that exhibits a repeating pattern which can be replicated at every scale." (Rohnn B Sanderson, "Understanding Chaos as an Indicator of Economic Stability", 2016) 

 "Geometric pattern repeated at progressively smaller scales, where each iteration is about a reproduction of the image to produce completely irregular shapes and surfaces that can not be represented by classical geometry. Fractals are generally self-similar (each section looks at all) and are not subordinated to a specific scale. They are used especially in the digital modeling of irregular patterns and structures in nature." (Mauro Chiarella, Folds and Refolds: Space Generation, Shapes, and Complex Components, 2016)

SQL Reloaded: The Power of Joins III (Vertical Joins)

Introduction 

 
      A vertical join allows the possibility of retrieving data from multiple datasets by combining the attributes from one or more datasets on the same row, being possible to include complex expressions using any combination of attributes. The join within a vertical join is based only on the attributes specified in the join constraint(s), typically each constraint taking the form of an identity, in this case the data types must match, though also complex expressions evaluated to a value of true/false could be used.

      Within SQL Server 2000 were possible two syntaxes for vertical joins – the ANSI and non-ANSI syntaxes, however in later versions the non-ANSI syntax could be enabled only by changing database’s compatibility level to 80, Microsoft recommends using only the ANSI standard because the non-ANSI syntax could be dropped in future versions. In ANSI syntax are used the LEFT OTER JOIN, RIGHT OUTER JOIN, INNER JOIN and FULL OUTER JOIN operators in the FROM clause while in non-ANSI syntax the join constraints appear in WHERE clause, being used the *= and =* operators for LEFT OUTER JOIN, respectively RIGHT OUTER JOIN, and = for an INNER JOIN, the FULL OUTER JOIN not being supported in non-ANSI. Starting with SQL Server 2005 were introduced also the CROSS APPLY and OUTER APPLY operators that could be used to model cross joins. 

-- Joins ANSI syntax 
SELECT A.Attribute1 
[, A.Attribute] 
[, B.Attribute] 
FROM TABLE1 A 
    [LEFT|RIGHT|FULL] [INNER|OUTER] TABLE2 B 
        ON <join_constraints> 
[WHERE <constraints>] 

-- Joins non-ANSI syntax 
SELECT A.Attribute1 
[, A.Attribute] 
[, B.Attribute] 
FROM TABLE1 A 
,TABLE2 B 
[WHERE<join_constraints>] 
[AND|OR <join_constraints>] 

Notes:
1.   In case of horizontal joins the Set Theory applies mainly to the join constraints, an element in the dataset being the n-uple formed by the attributes participating in the join constraints. Many times it’s natural to use the foreign key-primary key attribute pairs though tables’ design and the logic to be modeled don’t always allow this luxury, therefore when choosing the attributes participating in the join is targeted to find the smallest n-uple with unique values across the whole dataset. From a performance standpoint is preferred to use the attributes that are part of an index, actually in many cases an index arrives to be created for the attributes used often in joins in order to increase queries’ performance. If the n-uple used in the join doesn’t have unique values, in other words exists two records in the dataset on which the n-uple takes the same values for each attribute of the n-uple, then duplicates are induced in the join. 

2.    The records whose attributes participating in the join constraint have NULL values are ignored, so it might be needed to consider replacing the NULL values with a default value, though must be paid attention also to the possibility of introducing duplicates. 

3.    Oracle supports the SQL ANSI syntax together with a slightly different form of non-ANSI syntax.  Especially when considering the portability of code it makes sense to use  the SQL ANSI syntax in any RDBMS that supports it; I mention this aspect because many Oracle developers are still using the non-ANSI syntax. 

4.    In case an attribute is found in more than one table then it’s needed to use aliases for the tables in which the attribute is found or prefix the attribute with the table and schema name (e.g. Production.Product.Name). Actually from performance reasons it’s advisable to always use aliases, thus the database engine identifying easier the source table for each attribute. 

5.     In theory in the SELECT statement could include all the attributes from the tables participating in the join, though it’s recommendable to use only the attributes needed (when possible should be also avoided SELECT * constructs). For output’s readability it makes sense to group together the attributes coming from the same table or arrange them in a patterns that could be easily understood by the users. 

6.     The cross, inner and full outer joins are the only commutative operations, in other words the same results are obtained if the tables are inversed. It can be discussed also about associativity, the ability of changing the table join processing precedence without affecting the result, [1] for example discussing in detail this topic.

      For demonstrating the application of vertical joins I will use the Production.Product, Purchasing.PurchaseOrderDetail POD and HumanResources.Employee tables from AdventureWorks database.

The Inner Join 

 
    The INNER JOIN operators, shortened sometimes as JOIN, allows retrieving the rows matched from both tables based on the join constraints, thus if for one record isn’t found a match in the other table then the record will not appear in the result dataset. 

  

-- Inner Join ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
    JOIN Purchasing.PurchaseOrderDetail POD  
       ON ITM.ProductID = POD.ProductID 
WHERE ITM.MakeFlag = 0 

-- Inner Join non-ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
Purchasing.PurchaseOrderDetail POD 
WHERE ITM.ProductID=POD.ProductID 
    AND ITM.MakeFlag = 0 

Note:
      The inner join could be considered the projection of the intersection operation from Set Theory applied to the attributes participating in the join constraints.

      In order to exemplify what’s happening in the background I will use a smaller subset from each of the two tables used as input, and the final result for the inner join: 

 

   As can be seen from the above image, the 8th, 9th and 10th records from Purchase Orders sample table corresponding to PurchaseOrderID = 7 are not appearing in the result dataset because the corresponding Product IDs (317, 318 and 319) for the respective lines are not found in the Products sample table. Also the second line from Products sample table corresponding to ProductID = 2 is not appearing in the result dataset because there is no Purchase Order placed for the respective Product.

Note:
      The below query summarizes the sample tables used above and the output of the inner join, inline views being used for each of the tables in order to simplify the use of the example with all types of join, thus only the join type needs to be changed for exemplification: 

  

SELECT IsNull(ITM.ProductID, POD.ProductID) ProductID 
, POD.PurchaseOrderID 
, ITM.ProductNumber 
, ITM.StandardCost 
, POD.UnitPrice 
, POD.OrderQty 
FROM ( -- sample Products 
     SELECT ProductID 
     , ProductNumber 
     , StandardCost 
      FROM Production.Product 
      WHERE ProductID IN (1, 2, 359, 360, 530, 4, 512, 513) 
      AND MakeFlag = 0) ITM 
      JOIN (-- sample Purchase Orders 
          SELECT ProductID 
         , PurchaseOrderID 
         , UnitPrice 
         , OrderQty 
         FROM Purchasing.PurchaseOrderDetail 
         WHERE PurchaseOrderID IN (1,2,3,4,5,6,7)) POD 
     ON ITM.ProductID = POD.ProductID 
ORDER BY 2 

The Left Outer Join 

 
    The LEFT OUTER JOIN, shortened sometimes as LEFT JOIN, allows retrieving all the rows from the left table and only the matched records from the right table based on the join constraints.

-- Left Join ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
      LEFT JOIN Purchasing.PurchaseOrderDetail POD 
         ON ITM.ProductID = POD.ProductID 
WHERE ITM.MakeFlag = 0 

-- Left Join non-ANSI syntax 
SELECTITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
, Purchasing.PurchaseOrderDetail POD 
WHERE ITM.ProductID*=POD.ProductID 
    AND ITM.MakeFlag = 0   

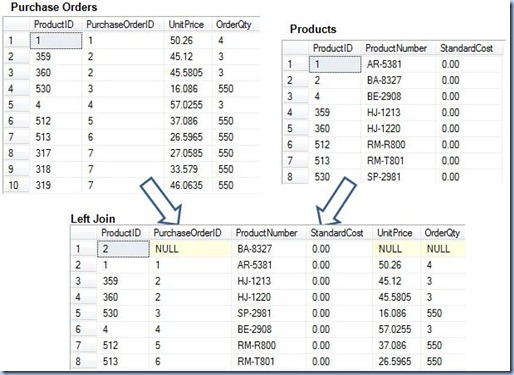
      In order to exemplify what’s happening in the background I will use a smaller subset from each of the two tables used as input, and the final result for the left outer join:   

 

    Because the Products sample table is used as row-preserving table it will be shown all the records it holds together with the matched records from the Purchase Orders sample table, thus the Purchase Orders sample table corresponding to PurchaseOrderID = 7 are not appearing in the result dataset because the corresponding Product IDs (317, 318 and 319) for the respective lines are not found in the Products sample table. 

     If the tables are inversed then the Purchase Orders table becomes the row-preserving table and thus all the records from it are shown, including the records for which no Product is found in the Products sample table.

Notes:
1.   The left join has no direct correspondent operation from Set Theory but it’s the projection of AU(A∩B) formula, which equals to (A\B)U(A∩B). The left join could be used also to determine the projection of A\B by adding in the WHERE clause the constraint that allows retrieving only the records for which no match was found to the right table: 

-- LEFT Join ANSI syntax for A\B 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
    LEFT JOIN Purchasing.PurchaseOrderDetail POD 
      ON ITM.ProductID = POD.ProductID 
WHERE POD.ProductID IS NULL 

2.    Special attention must be given to the way the join and non-join constraints are added to the WHERE clause, because if the constraint is based solely on the null-supplying table and included in the WHERE clause without handling the Null case then an inner join could have been written instead because the rows for the attributes participating in constraints are ignored. In order to preserve left join’s character the constraint should be brought into the join constraint as below: 

-- Right Join ANSI syntax modified 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Purchasing.PurchaseOrderDetail POD 
     LEFT JOIN Production.Product ITM 
        ON ITM.ProductID = POD.ProductID 
AND ITM.MakeFlag = 0 

 
      Because unlike in Oracle the both terms of an non-ANSI left join operator must contain columns (attributes), then the IsNull function could be used in order to handle the NULL values:   

SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROMPurchasing.PurchaseOrderDetail POD 
, Production.Product ITM 
WHERE POD.ProductID *= ITM.ProductID 
AND IsNull(ITM.MakeFlag, 0) = 0   

      The same method could be used also to keep non-join constraints in the WHERE clause when using the ANSI syntax for outer joins. 

3.    There are cases in which is needed to replace with default values the NULL values from the not matched records from the Null-preserving table.

The Right Outer Join 

    The RIGHT OUTER JOIN, shortened sometimes as RIGHT JOIN, allows retrieving all the rows from the right table and only the matched records from the right table based on the join constraints. A left join could be rewritten as a right join, just by inversing the tables, in fact the above examples given for left joins are rewritten using a right join:   

-- Right Join ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Purchasing.PurchaseOrderDetail POD 
     RIGHT JOIN Production.Product ITM 
          ON ITM.ProductID = POD.ProductID 
WHERE ITM.MakeFlag = 0 

-- Right Join ANSI syntax modified 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Purchasing.PurchaseOrderDetail POD 
    RIGHT JOIN Production.Product ITM 
         ON ITM.ProductID = POD.ProductID 
AND ITM.MakeFlag = 0  

   In order to exemplify what’s happening in the background I will use a smaller subset from each of the two tables used as input, and the final result for the right outer join: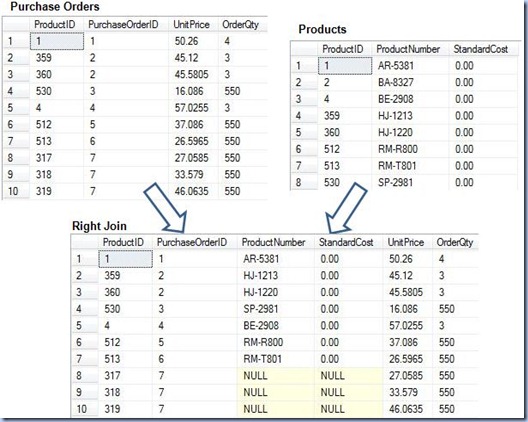

     As opposed to the general syntax examples given above for the left outer join in which the Products sample table is used as row-preserving table, in the above image the Purchase Orders sample table is used as row-preserving table, thus are shown all the records it holds and only the matched Products.

The Full Outer Join   

    The FULL OUTER JOIN, shortened sometimes as FULL JOIN, allows retrieving the rows matched from both tables based on the join together with the not matched records from both tables.

-- Full Outer Join ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
    FULL JOIN Purchasing.PurchaseOrderDetail POD 
       ON ITM.ProductID = POD.ProductID  

   In order to exemplify what’s happening in the background I will use a smaller subset from each of the two tables used as input, and the final result for the full outer join:

  As can be seen from the above image are considered all the rows from both tables, including the Purchase Orders for which no match was found in the Products sample table and the Products for which no Purchase Order is found in the corresponding sample table.  

Note:
1.      As in the left outer join’s case, special attention must be given to the non-join constraints added in the WHERE clause because they could reduce the range of applicability of the full outer join to a left/right outer join or to an inner join. Eventually, if really needed to add non-join constraints, instead of the base table it could be used an inline view as input for the full outer join.   

2.      In SQL Server there is no non-ANSI operator equivalent to the ANSI full outer join operator, though the same functionality could be obtained by using the union between the result of a left outer join and the one of a right outer join:

-- Full Outer Join non-ANSI syntax equivalent 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
, Purchasing.PurchaseOrderDetail POD 
WHERE ITM.ProductID *= POD.ProductID 
UNION 
SELECT 
ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
, Purchasing.PurchaseOrderDetail POD 
WHERE ITM.ProductID =* POD.ProductID 

    In some cases could be useful to rewrite the above query using the ANSI syntax, but this time it makes sense to use the UNION ALL operator instead and limit the second dataset only to the Products for which no Purchase Order was placed:   

-- Full Outer Join ANSI syntax equivalent using Left & Right Outer Joins 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
     LEFT JOIN Purchasing.PurchaseOrderDetail POD  
         ON ITM.ProductID = POD.ProductID 
UNIONALL 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
      RIGHT JOIN Purchasing.PurchaseOrderDetail POD  
            ON ITM.ProductID = POD.ProductID 
WHERE ITM.ProductID IS NULL 

The Cross Join 

    The CROSS JOIN resumes at listing the joined tables without specifying the join constraint and it returns the carthezian product between the two tables, a row from the first table being matched to each row from the second table, thus if the first table has m rows and the second n rows, the final query will return m*n rows. If in non-ANSI syntax it’s pretty simple to create a cross join, using ANSI syntax the same could be obtained using a full outer join with a join constraint that always equates to true independently of the tables’ attributes values (e.g. 1=1) or, starting with SQL Server 2005,  when was first introduced, could be used the cross apply operator.   

-- Cross Join ANSI syntax (CROSS APPLY) 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
     CROSS APPLY Purchasing.PurchaseOrderDetail POD 

-- Cross Join ANSI syntax (FULL OUTER JOIN) 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
    FULL OUTER JOIN Purchasing.PurchaseOrderDetail POD 
      ON 1=1 

-- Cross Join non-ANSI syntax 
SELECT ITM.ProductID 
, POD.PurchaseOrderID 
FROM Production.Product ITM 
, Purchasing.PurchaseOrderDetail POD 

The Self Join   

     The self join is a special type of vertical join in which the left and right tables in a join represent the same table, and it could take the form of any of the above mentioned types of joins. This typically implies the existence of a self-reference attribute that references the primary key of another record, such structures being useful in modeling hierarchies (e.g. Bill of Materials, Human Resources hierarchies). For example HumanResources.Employee table stores together with the current Employee also ManagerID which stores the EmployeeID of Employee’s Manager, that stores at its turn the reference to Manager’s Manager, thus a whole structure of an organization could be built with self joins. The simplified queries for getting the Manager of Employee’s Manager could be written with a left join, this mainly because there might be Employees who don’t have a manager:   

-- Self Join ANSI Syntax (LEFT JOIN) 
SELECT EMP.EmployeeID 
, EMP.ManagerID 
, MNG.ManagerID ManagersManagerID 
FROM HumanResources.Employee EMP 
    LEFT JOIN HumanResources.Employee MNG 
       ON EMP.ManagerID = MNG.EmployeeID 

-- Self Join non-ANSI Syntax (LEFT JOIN) 
SELECT EMP.EmployeeID 
, EMP.ManagerID 
, MNG.ManagerID ManagersManagerID 
FROM HumanResources.Employee EMP 
, HumanResources.Employee MNG 
WHERE EMP.ManagerID *= MNG.EmployeeID 

Note:
       In order to built the whole hierarchy, starting with SQL Server 2005 instead of using multiple self joins could be used common tables expressions (CTE), they offering more flexibility and better performance.

References:
[1] David M.M., (1999). Advanced ANSI SQL Data Modeling and Structure Processing. Artech House. ISBN: 1-58053-038-9

SQL Reloaded: The Power of Joins II (Horizontal Joins)

Introduction 

 
    A horizontal join allows retrieving data from two or more datasets by merging/comparing the rows from each involved dataset, the join of rows being done on vertical, thus a row from the final result dataset containing only the attributes from one of the input datasets, the attributes being matched based on their order in the dataset (first attribute with first attribute from each dataset, second with the second, and so on), the output attribute taking the name of the correspondent attribute from the first. It worth to mention that the comparison is done at row level, thus we could talk about distinct rows if at least one of the attributes is having different values.

    There are two important constraints horizontal joins comes with: the datasets involved in a vertical join must have the same number of attributes and the joined attributes must have the same data type. If one of the attributes is not available in one of the datasets, a NULL or other default value could be provided for the missing attribute, while in case data types can’t be converted implicitly then the conversion must be done explicitly to a data type sufficient to accommodate the data type of the attributes joined under the same attribute.
  
      The general syntax for an horizontal join could be written as follows: 

-- Horizontal Join syntax 
SELECT A.Attribute1 
[, A.Attribute] 
FROM TABLE1 A 
[WHERE <constraints>] 
UNION | INTERSECT | EXCEPT [ALL] 
SELECT B.Attribute1 
[, B.Attribute] 
FROM TABLE2 B 
[WHERE <join_constraints>]  
[ORDER BY <order_attributes>] 

Notes:   

1.    There are 3 horizontal join operators UNION for union (AUB), INTERSECT (A∩B) for intersection and EXCEPT for subtraction (A\B), and only UNION could be used in combination with ALL keyword in order to show ignore the duplicates. Please note that only the union and intersection operators are commutative: AUB = BUA, respectively A∩B = B∩A, while A\B<>B\A. 

 
2.    The SELECT statement for each dataset could include any complex logic supported, including aggregates, window ranking and aggregate functions, virtual tables (views, user-defined functions), vertical joins, etc. 

 
3.     The horizontal join may contain only one ORDER BY clause placed at the end of the query, and with it could be used directly the attributes’ name or alias given to the columns from first dataset. In case aliases are used, and especially when many attributes are involved or then when the attribute involve complex logic, it makes sense to use the same alias also for the other datasets involved in the join.

   For demonstrating the horizontal operations I will use the following two datasets based on the same table, respectively Products table from AdventureWorks database. 

 

-- Dataset A 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 200 

-- Dataset B 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 250 

The UNION Join 

    The UNION join, also referred as the outer union, allows combining two datasets in one dataset formed from the combined rows of each data set, the eventual duplicate rows being eliminated. In case are needed also the duplicates, then the ALL keyword could be used in combination with the UNION (also referred as UNION ALL operator), this technique being recommended when the two datasets have no common records because when a simple UNION is used the database engine still checks for duplicates. 

-- UNION example (AUB) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 200 
UNION 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 250  

Note:         
     Because the above two datasets are using the same table the final output is the same with the output of the below query, the reunion being thus applied directly to the constraints used. It is actually recommended to avoid using unions:

-- alternative for UNION example (AUB) 
SELECTITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 250 

      In order to exemplify what’s happening in the background I will use only two rows from each of the two datasets used as input, on the right side being shown the output of applying the UNION, respectively UNION ALL operators:

The INTERSECT Join 

 
    The INTERSECT operator combines the two datasets in one dataset formed from the rows found to be present in both datasets. 

 

-- INTERSECT example (A∩B) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 200 
INTERSECT 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 250 

Note:
   Because the above two datasets are using the same table the final output is the same with the output of the following query, the intersection could be thus applied directly to the constraints used: 

  

-- alternative for INTERSECT example (A∩B) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 200 

     In order to exemplify what’s happening in the background I will use only two rows from each of the two datasets used as input, on the right side being shown the output of applying the INTERSECT operator:
 
The EXCEPT Join 

-- EXCEPT example (A\B) 
SELECTITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 200 
EXCEPT 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
,ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 250 

-- EXCEPT example (B\A) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 250 
EXCEPT 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 200 

   As can be seen from the above two examples there are two possibilities of subtracting two datasets – A\B, respectively B\A, selecting the rows which are only in A and not in B, respectively the rows which are in B and not in A.

Note:
   Because the above two datasets are using the same table the final output is the same with the output of the following queries, the subtraction could be thus applied directly to the constraints used: 

-- alternative for SUBTRACTION example (A\B) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost 
, ITM.MakeFlag 
FROM Production.Product ITM 
WHERE ITM.StandardCost >= 0 
    AND ITM.StandardCost < 100 

-- alternative for SUBTRACTION example (B\A) 
SELECT ITM.ProductID 
, ITM.Name ProductName 
, ITM.ProductNumber 
, ITM.StandardCost , ITM.MakeFlag 
FROMProduction.Product ITM 
WHERE ITM.StandardCost > 200 
    AND ITM.StandardCost <= 250 

      In order to exemplify what’s happening in the background I will use only two rows from each of the two datasets used as input, on the right side being shown the output of applying the EXCEPT for A\B, respectively B\A: 

 


Combining Operators 

 
    For the sake of simplicity all the above exemplifications are using only two datasets, though multiple datasets could be joined in this way, here is an example for the UNION ALL based on three datasets (please note that I avoided to list the attributes): 

 

-- multiple UNION 
SELECT * 
FROMProduction.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 50 
UNION ALL
SELECT * 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 100 AND 150 
UNION ALL 
SELECT * 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 200 AND 250 

Note:
     Also in this case the union could be applied directly on the constraints, though because there is no overlap between any combination of the three ranges, the constraint needs to be modified accordingly: 

  
-- multiple UNION 
SELECT * 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 0 AND 50 
    OR ITM.StandardCost BETWEEN 100 AND 150 
    OR ITM.StandardCost BETWEEN 200 AND 250 

    When the union and intersection operations are used with multiple datasets it doesn’t matter the order of the datasets because the two operations are associative: (AUB)UC=AU(BUC)=AUBUC, respectively (A∩B)∩C=A∩(B∩C)=A∩B∩C, though not the same could be said about subtraction because (A\B)\C <> A\(B\C) or the cases in which operators are combined, for example (A\B)UC<>A\(BUC), so is needed to use parentheses in order to avoid eventual surprises. 

  

-- (A\B)UC 
( 
    -- subtraction 
    SELECT * 
    FROM Production.Product ITM 
    WHERE ITM.StandardCost BETWEEN 0 AND 150 
    EXCEPT 
    SELECT * 
    FROM Production.Product ITM 
    WHERE ITM.StandardCost BETWEEN 100 AND 150 
) 
UNION 
SELECT * 
FROM Production.Product ITM 
WHERE ITM.StandardCost BETWEEN 150 AND 250 

Note:
      Knowing the basics of Set Theory is important in making your queries returning the expected results, the use of some of the identities allowing to simplify considerably the queries sometimes. Without a set-mindset I think it will be difficult to solve such problems.

The Power of Joins – Part I: Introduction

     Joins are the heart of RDBMS, they allowing to retrieve data (bring data together in a single result dataset) from multiple (related) table-like objects (tables, views, user-defined functions) by defining how and which  records are selected from such objects. In order to reduce the complexity of such a topic I will introduce the joins with regard to tables, the concepts applying also to views and user-defined functions, especially when they are regarded as “virtual” tables. In theory any two tables could be joined independently on whether a direct or indirect relation exists between them, it can be a foreign key, a natural key, a date or any other attribute that could be used to get a certain view into the data. Typically a join involves a minimum of two tables, but before going dipper into the topic it makes sense to look a little at the various terms used to refer to the tables joined and the anatomy of a join.

     There are various ways of naming the tables involved in a join:
- left vs. right tables, where the left table is the first listed table participating in the join and the right table the second listed table participating in the join;
- parent vs. dependent tables, refers to tables between which exists a direct relationship, in other words exists a primary key and a foreign key, the dependent table being the table containing the foreign key, and the parent table the table containing the primary key;
- parent vs. child tables, is similar with the previous definition, the child table being an alternative naming for the dependent table, in addition we can talk also about grandchildren when a child table is referenced at its turn by other table called thus, when the three tables are considered together, the grandchild table;
- referent vs. referenced tables, another alternative for naming the tables between which exists a direct relationship, the referenced table being the table containing the foreign key, and the referent table the ones containing the primary key;
- inner vs. outer tables, these terms are used only in the case of outer joins, the inner table being the table from which are selected all the records, while the outer table is the table from which are selected only the matched records, therefore the two are also called sometimes the row-preserving table, respectively the null-supplying table;

      None of the above pair of naming conventions are perfect because they can’t be used to address all the join situations in which tables are involved, and some of the terms may be used interchangely, especially when a term is preferred in order to send across adequate meaning, for example referring to a table as a inner table then we imply also that we deal with a left or right join. I realized that in time I used all the the above terms in a situation or another, however I prefer to use the left vs. right tables denomination, and occasionally inner vs. outer tables when referring to left or right joins.

     In addition to the two tables joined a query typically includes also a join operator that specifies the join type (union, inner, outer or cross join), the join constraints that specifies which attributes are used to join the tables and the logical operators used, and eventually the non-join constraints referring to other constraints than the join constraints. I’m saying typically because either of the two could be missing, thus if the the join constraint and operator miss then we deal with a carthezian join, while if the join constraint is appearing in the WHERE instead of FROM clause then there is no need to specify the join operator or in case of a UNION there is no need to specify the join constraint, though I will come back later on this topic.

      The work with joins is deeply rooted in the Set Theory (the tables joined referred also as datasets) and the set operations – union, subtraction and intersection, their projection in world of databases coming, from my point of view and not sure if the database literature really discusses about this, into two flavors – vertical vs. horizontal joining. By vertical joining I’m referring to the intrinsic character of joins, in the result dataset the attributes from the two joined datasets appearing on the same row, while in the horizontal joining they never appear on the same row, thus a row being formed exclusively from the records of only one of the tables involved in the join. Thus we can discuss about vertical/horizontal joins as projection of union, intersection and subtraction operations, each of them with different connotations, the horizontal operations being actually similar to the ones from set theory. If we discuss about joins then we inevitably we have to mention also the anti-joins and semi-joins, a special type of queries based on NOT IN, respectively EXISTS operators.

DBMS: Relational Model (Definitions)

"A method of organizing data into two-dimensional tables made up of rows and columns. The model is based on the mathematical theory of relations, a part of set theory." (Microsoft Corporation, "SQL Server 7.0 System Administration Training Kit", 1999)

"A model that provides a two-dimensional structure to data. The relational database model more or less throws out the window the concept and restriction of a hierarchical structure, but does not completely abandon data hierarchies. Any table can be accessed directly with having to access all parent objects. Precise data values (such as primary keys) are required to facilitate skirting the hierarchy (to find individual records) in specific tables." (Gavin Powell, "Beginning Database Design", 2006)

"A paradigm for describing the structure of a database in which entities are represented as tables, and relationships between the entities are represented by matching data." (Jan L Harrington, "Relational Database Design and Implementation" 3rd Ed., 2009)

"The relational model, based on mathematical set theory, represents data as independent relations. Each relation (table) is conceptually represented as a matrix of intersecting rows and columns. The relations are related to each other through the sharing of common entity characteristics (values in columns)." (Carlos Coronel et al, "Database Systems: Design, Implementation, and Management" 9th Ed., 2011)

"A database model based on first-order predicate logic [...]" (Craig S Mullins, "Database Administration: The Complete Guide to DBA Practices and Procedures", 2012)

"A form of data where data is normalized" (Daniel Linstedt & W H Inmon, "Data Architecture: A Primer for the Data Scientist", 2014)

"A type of model that aims to identify relationships of interest and quantify the strength of relationship between individuals or entities. Common examples include market basket analysis and social network analysis." (Evan Stubbs, "Big Data, Big Innovation", 2014)

"Data represented as a set of related tables or relations." (Jeffrey A Hoffer et al, "Modern Systems Analysis and Design" 7th Ed., 2014)

"A database model in which data and the relationships among them are organized into tables" (Nell Dale & John Lewis, "Computer Science Illuminated" 6th Ed., 2015)

"Relational modeling is a popular data modeling technique to reduce the duplication of data and ensure the referential integrity of the data." (Piethein Strengholt, "Data Management at Scale", 2020)

"(1) A data model whose pattern or organization is based on a set of relations, each of which consists of an unordered set of tuples. (2) A data model that provides for the expression of relationships among data elements as formal mathematical relations." (IEEE 610.5-1990)

Lists, Sets and a Little Math

In the previous post I've shown how a delimited list can be transformed in a table with the help of table-valued functions, and I gave as example a JOIN which provided the common elements between two lists:

-- intersection of two sets
SELECT A.* 
FROM dbo.SplitList('23 34 50 71', ' ') A 
     JOIN dbo.SplitList('23,34,25,45', ',') B 
    ON A.Value = B.Value 

A list is a collection of elements which can repeat in the list. When the elements of a list don't repeat we can talk about a set. Sets considered in combination with reunion, intersection, (set) difference, cartesian product and power set forms the basis of topology, however the most interesting part is when we start taking elements from the set or combining the elements of sets.

Arrangements with repetition, called also n-tuples of m-sets, given the fact that the arrangements are created by taking n elements from m sets. The number of elements is given by the formula: m^n. Thus, the arrangements of 2, 3, 4 elements with repetition will give 16, 64, respectively 256 combinations:

 -- arrangements of 2 elements with repetition
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
    , dbo.SplitList('1,2,3,4', ',') B 

 ORDER BY A.Value, B.Value 
 
 -- arrangements of 3 elements with repetition
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
    , dbo.SplitList('1,2,3,4', ',') B
    , dbo.SplitList('1,2,3,4', ',') C 

 ORDER BY A.Value, B.Value, C.Value

 -- arrangements of 4 elements with repetition
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
    , dbo.SplitList('1,2,3,4', ',') B 
    , dbo.SplitList('1,2,3,4', ',') C 
    , dbo.SplitList('1,2,3,4', ',') D 

ORDER BY A.Value, B.Value, C.Value, D.Value 

Combinations are selections of items, such that the order of selection does not matter, though the elements don't repeat inside of the n-tuple. Combinations of 4 elements taken as 2, 3, respectively 4:

 -- combinations of 4 elements taken as 2
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
      JOIN  dbo.SplitList('1,2,3,4', ',') B  
        ON A.Value < B.Value 

 ORDER BY A.Value, B.Value
 
 -- combinations of 4 elements taken as 3
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
       JOIN dbo.SplitList('1,2,3,4', ',') B
  ON A.Value < B.Value 
            JOIN  dbo.SplitList('1,2,3,4', ',') C 
       ON B.Value < C.Value 

 ORDER BY A.Value, B.Value, C.Value

 -- combinations of 4 elements taken as 4
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
      JOIN dbo.SplitList('1,2,3,4', ',') B 
 ON A.Value < B.Value 
           JOIN dbo.SplitList('1,2,3,4', ',') C 
      ON B.Value < C.Value 
                JOIN dbo.SplitList('1,2,3,4', ',') D 
    ON C.Value < D.Value 

 ORDER BY A.Value, B.Value, C.Value, D.Value 

Permutations, in exchange, involve arranging the elements of a set by interchanging their position. The permutations of 4 elements are given by following code:

 -- permutations of 4 elements 
 SELECT * 
 FROM dbo.SplitList('1,2,3,4', ',') A 
      JOIN dbo.SplitList('1,2,3,4', ',') B 
 ON A.Value <> B.Value 
           JOIN dbo.SplitList('1,2,3,4', ',') C 
             ON B.Value <> C.Value 
     AND A.Value <> C.Value 
         JOIN dbo.SplitList('1,2,3,4', ',') D 
    ON C.Value <> D.Value 
          AND B.Value <> D.Value 
   AND A.Value <> D.Value 
 ORDER BY A.Value, B.Value, C.Value, D.Value 

In praxis there are specific algorithms for generating the arrangements, combinations or permutations of a set, however I think that the above examples are simpler to understand as they reflect also the mathematical heuristic. The downside is that the complexity of the queries increases with the number of elements in the set.

In the end here's a fun example on how simple propositions can be created:

 -- creating propositions
 SELECT 'The ' + A.Value + ' ' + B.Value + ' ' + C.Value + '!' 
 FROM dbo.SplitList('cat,dog,bird,fish', ',') A 
    , dbo.SplitList('drinks,smells,eats,jumps', ',') B 
    , dbo.SplitList('loudly,nicely,grumpy,alone', ',') C 

Happy Coding!