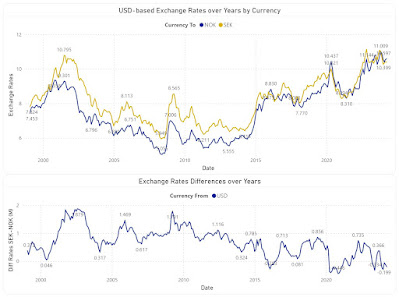
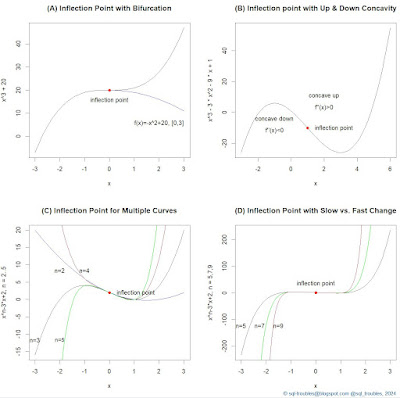
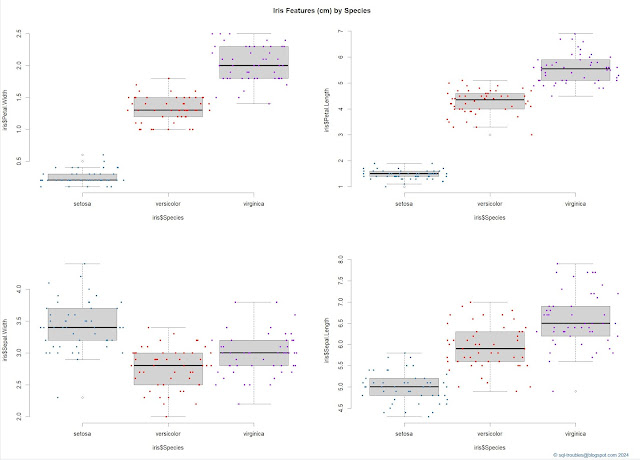
"Generally speaking, the plotting of a curve consists of graphically representing numbers and equations by the relation of points and lines with reference to other given lines or to a given point." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"Since a table is a collection of certain sets of data, a chart with one curve representing each set of data can be made to take the place of the table. Wherever a chart can be plotted by straight lines, the speed of this is infinitely greater than making out a table, and where the curvilinear law is known, or can be approximated by the use of the empiric law, the speed is but little less." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"In working through graphics one has, however, to be exceedingly cautious in certain particulars, for instance, when a set of figures, dynamical or financial, are available they are, so long as they are tabulated, instinctively taken merely at their face value. When plotted, however, there is a temptation to extrapolation which is well nigh irresistible to the untrained mind. Sometimes the process can be safely employed, but it requires a rather comprehensive knowledge of the facts that lie back of the data to tell when to go ahead and when to stop." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"The wandering of a line is more powerful in its effect on the mind than a tabulated statement; it shows what is happening and what is likely to take place just as quickly as the eye is capable of working." (A Lester Boddington, "Statistics And Their Application To Commerce", 1921)
"For most line charts the maximum number of plotted lines should not exceed five; three or fewer is the ideal number. When multiple plotted lines are shown each line should be differentiated by using (a) a different type of line and/or (b) different plotting marks, if shown, and (c) clearly differentiated labeling." (Robert Lefferts, "Elements of Graphics: How to prepare charts and graphs for effective reports", 1981)
"The information on a plot should be relevant to the goals of the analysis. This means that in choosing graphical methods we should match the capabilities of the methods to our needs in the context of each application. [...] Scatter plots, with the views carefully selected as in draftsman's displays, casement displays, and multiwindow plots, are likely to be more informative. We must be careful, however, not to confuse what is relevant with what we expect or want to find. Often wholly unexpected phenomena constitute our most important findings." (John M Chambers et al, "Graphical Methods for Data Analysis", 1983)
"The quantile plot is a good general display since it is fairly easy to construct and does a good job of portraying many aspects of a distribution. Three convenient features of the plot are the following: First, in constructing it, we do not make any arbitrary choices of parameter values or cell boundaries [...] and no models for the data are fitted or assumed. Second, like a table, it is not a summary but a display of all the data. Third, on the quantile plot every point is plotted at a distinct location, even if there are duplicates in the data. The number of points that can be portrayed without overlap is limited only by the resolution of the plotting device. For a high resolution device several hundred points distinguished." (John M Chambers et al, "Graphical Methods for Data Analysis", 1983)
"The time-series plot is the most frequently used form of graphic design. With one dimension marching along to the regular rhythm of seconds, minutes, hours, days, weeks, months, years, centuries, or millennia, the natural ordering of the time scale gives this design a strength and efficiency of interpretation found in no other graphic arrangement." (Edward R Tufte, "The Visual Display of Quantitative Information", 1983)
"We can gain further insight into what makes good plots by thinking about the process of visual perception. The eye can assimilate large amounts of visual information, perceive unanticipated structure, and recognize complex patterns; however, certain kinds of patterns are more readily perceived than others. If we thoroughly understood the interaction between the brain, eye, and picture, we could organize displays to take advantage of the things that the eye and brain do best, so that the potentially most important patterns are associated with the most easily perceived visual aspects in the display." (John M Chambers et al, "Graphical Methods for Data Analysis", 1983)
"As a general rule, plotted points and graph lines should be given more 'weight' than the axes. In this way the 'meat' will be easily distinguishable from the 'bones'. Furthermore, an illustration composed of lines of unequal weights is always more attractive than one in which all the lines are of uniform thickness. It may not always be possible to emphasise the data in this way however. In a scattergram, for example, the more plotted points there are, the smaller they may need to be and this will give them a lighter appearance. Similarly, the more curves there are on a graph, the thinner the lines may need to be. In both cases, the axes may look better if they are drawn with a somewhat bolder line so that they are easily distinguishable from the data." (Linda Reynolds & Doig Simmonds, "Presentation of Data in Science" 4th Ed, 1984)
"The plotted points on a graph should always be made to stand out well. They are, after all, the most important feature of a graph, since any lines linking them are nearly always a matter of conjecture. These lines should stop just short of the plotted points so that the latter are emphasised by the space surrounding them. Where a point happens to fall on an axis line, the axis should be broken for a short distance on either side of the point." (Linda Reynolds & Doig Simmonds, "Presentation of Data in Science" 4th Ed, 1984)
"Boxplots provide information at a glance about center (median), spread (interquartile range), symmetry, and outliers. With practice they are easy to read and are especially useful for quick comparisons of two or more distributions. Sometimes unexpected features such as outliers, skew, or differences in spread are made obvious by boxplots but might otherwise go unnoticed." (Lawrence C Hamilton, "Regression with Graphics: A second course in applied statistics", 1991)
"The scatterplot is a useful exploratory method for providing a first look at bivariate data to see how they are distributed throughout the plane, for example, to see clusters of points, outliers, and so forth." (William S Cleveland, "Visualizing Data", 1993)
"Construction refers to everything involved in the production
of the graphical display, including questions of what to plot and how to plot.
Deciding what to plot is not always easy and again depends on what we want to
accomplish. In the initial phases of an analysis, two-dimensional displays of
the response against each of the p predictors are obvious choices for gaining
insights about the data, choices that are often recommended in the introductory
regression literature. Displays of residuals from an initial exploratory fit
are frequently used as well." (R Dennis Cook, "Regression Graphics: Ideas for
studying regressions through graphics", 1998)
"If you want to show the growth of numbers which tend to grow by percentages, plot them on a logarithmic vertical scale. When plotted against a logarithmic vertical axis, equal percentage changes take up equal distances on the vertical axis. Thus, a constant annual percentage rate of change will plot as a straight line. The vertical scale on a logarithmic chart does not start at zero, as it shows the ratio of values (in this case, land values), and dividing by zero is impossible." (Herbert F Spirer et al, "Misused Statistics" 2nd Ed, 1998)
"A bar graph typically presents either averages or frequencies. It is relatively simple to present raw data (in the form of dot plots or box plots). Such plots provide much more information. and they are closer to the original data. If the bar graph categories are linked in some way - for example, doses of treatments - then a line graph will be much more informative. Very complicated bar graphs containing adjacent bars are very difficult to grasp. If the bar graph represents frequencies. and the abscissa values can be ordered, then a line graph will be much more informative and will have substantially reduced chart junk." (Gerald van Belle, "Statistical Rules of Thumb", 2002)
"Three key aspects of presenting high dimensional data are: rendering, manipulation, and linking. Rendering determines what is to be plotted, manipulation determines the structure of the relationships, and linking determines what information will be shared between plots or sections of the graph." (Gerald van Belle, "Statistical Rules of Thumb", 2002)
"Merely drawing a plot does not constitute visualization. Visualization is about conveying important information to the reader accurately. It should reveal information that is in the data and should not impose structure on the data." (Robert Gentleman, "Bioinformatics and Computational Biology Solutions using R and Bioconductor", 2005)
"A useful feature of a stem plot is that the values maintain their natural order, while at the same time they are laid out in a way that emphasises the overall distribution of where the values are concentrated (that is, where the longer branches are). This enables you easily to pick out key values such as the median and quartiles." (Alan Graham, "Developing Thinking in Statistics", 2006)
"Symmetry and skewness can be judged, but boxplots are not entirely useful for judging shape. It is not possible to use a boxplot to judge whether or not a dataset is bell-shaped, nor is it possible to judge whether or not a dataset may be bimodal." (Jessica M Utts & Robert F Heckard, "Mind on Statistics", 2007)
"Plotting data is a useful first stage to any analysis and will show extreme observations together with any discernible patterns. In addition the relative sizes of categories are easier to see in a diagram (bar chart or pie chart) than in a table. Graphs are useful as they can be assimilated quickly, and are particularly helpful when presenting information to an audience. Tables can be useful for displaying information about many variables at once, while graphs can be useful for showing multiple observations on groups or individuals. Although there are no hard and fast rules about when to use a graph and when to use a table, in the context of a report or a paper it is often best to use tables so that the reader can scrutinise the numbers directly." (Jenny Freeman et al, "How to Display Data", 2008)
"There are two main reasons for using graphic displays of datasets: either to present or to explore data. Presenting data involves deciding what information you want to convey and drawing a display appropriate for the content and for the intended audience. [...] Exploring data is a much more individual matter, using graphics to find information and to generate ideas. Many displays may be drawn. They can be changed at will or discarded and new versions prepared, so generally no one plot is especially important, and they all have a short life span." (Antony Unwin, "Good Graphics?" [in "Handbook of Data Visualization"], 2008)
"No other statistical graphic can hold so much information at a time than the parallel coordinate plot. Thus this plot is ideal to get an initial overview of a dataset, or at the very least a large subgroup of the variables." (Martin Theus & Simon Urbanek, "Interactive Graphics for Data Analysis: Principles and Examples", 2009)
"Spineplots have the nice property that highlighted proportions can be compared directly. However, it must be noted that the x axis in a spinogram is no longer linear. It is only piecewise linear within the bars. Although this might be confusing at first sight, it yields two interesting characteristics. Areas where only very few cases have been observed are squeezed together and thus get less visual weight. [...] Spineplots use normalized bar lengths while the bar widths are proportional to the number of cases in the category" (Martin Theus & Simon Urbanek, "Interactive Graphics for Data Analysis: Principles and Examples", 2009)
"Need to consider outliers as they can affect statistics such as means, standard deviations, and correlations. They can either be explained, deleted, or accommodated (using either robust statistics or obtaining additional data to fill-in). Can be detected by methods such as box plots, scatterplots, histograms or frequency distributions." (Randall E Schumacker & Richard G Lomax, "A Beginner’s Guide to Structural Equation Modeling" 3rd Ed., 2010)
"[...] if you want to show change through time, use a time-series chart; if you need to compare, use a bar chart; or to display correlation, use a scatter-plot - because some of these rules make good common sense." (Alberto Cairo, "The Functional Art", 2011)
"Visualization is what happens when you make the jump from raw data to bar graphs, line charts, and dot plots. […] In its most basic form, visualization is simply mapping data to geometry and color. It works because your brain is wired to find patterns, and you can switch back and forth between the visual and the numbers it represents. This is the important bit. You must make sure that the essence of the data isn’t lost in that back and forth between visual and the value it represents because if you can’t map back to the data, the visualization is just a bunch of shapes." (Nathan Yau, "Data Points: Visualization That Means Something", 2013)
"The term shrinkage is used in regression modeling to denote two ideas. The first meaning relates to the slope of a calibration plot, which is a plot of observed responses against predicted responses. When a dataset is used to fit the model parameters as well as to obtain the calibration plot, the usual estimation process will force the slope of observed versus predicted values to be one. When, however, parameter estimates are derived from one dataset and then applied to predict outcomes on an independent dataset, overfitting will cause the slope of the calibration plot (i.e., the shrinkage factor ) to be less than one, a result of regression to the mean. Typically, low predictions will be too low and high predictions too high. Predictions near the mean predicted value will usually be quite accurate. The second meaning of shrinkage is a statistical estimation method that preshrinks regression coefficients towards zero so that the calibration plot for new data will not need shrinkage as its calibration slope will be one." (Frank E. Harrell Jr., "Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis" 2nd Ed, 2015)
"A boxplot is a dotplot enhanced with a schematic that provides information about the center and spread of the data, including the median, quartiles, and so on. This is a very useful way of summarizing a variable's distribution. The dotplot can also be enhanced with a diamond-shaped schematic portraying the mean and standard deviation (or the standard error of the mean)." (Forrest W Young et al, "Visual Statistics: Seeing data with dynamic interactive graphics", 2016)
"A scatterplot reveals the strength and shape of the relationship between a pair of variables. A scatterplot represents the two variables by axes drawn at right angles to each other, showing the observations as a cloud of points, each point located according to its values on the two variables. Various lines can be added to the plot to help guide our search for understanding." (Forrest W Young et al, "Visual Statistics: Seeing data with dynamic interactive graphics", 2016)
"The most accurate but least interpretable form of data presentation is to make a table, showing every single value. But it is difficult or impossible for most people to detect patterns and trends in such data, and so we rely on graphs and charts. Graphs come in two broad types: Either they represent every data point visually (as in a scatter plot) or they implement a form of data reduction in which we summarize the data, looking, for example, only at means or medians." (Daniel J Levitin, "Weaponized Lies", 2017)
"With time series though, there is absolutely no substitute for plotting. The pertinent pattern might end up being a sharp spike followed by a gentle taper down. Or, maybe there are weird plateaus. There could be noisy spikes that have to be filtered out. A good way to look at it is this: means and standard deviations are based on the naïve assumption that data follows pretty bell curves, but there is no corresponding 'default' assumption for time series data (at least, not one that works well with any frequency), so you always have to look at the data to get a sense of what’s normal. [...] Along the lines of figuring out what patterns to expect, when you are exploring time series data, it is immensely useful to be able to zoom in and out." (Field Cady, "The Data Science Handbook", 2017)
