Graphical Representation: Graphics We Live By (Part III: Exchange Rates in Power BI)

Graphical Representation Series

An exchange rate (XR) is the rate at which one currency will be exchanged for another currency, and thus XRs are used in everything related to trades, several processes in Finance relying on them. There are various sources for the XR like the European Central Bank (ECB) that provide the row data and various analyses including graphical representations varying in complexity. Conversely, XRs' processing offers some opportunities for learning techniques for data visualization. 

On ECB there are monthly, yearly, daily and biannually XRs from EUR to the various currencies which by triangulation allow to create XRs for any of the currencies involved. If N currencies are involved for one time unit in the process (e.g. N-1 XRs) , the triangulation generates NxN values for only one time division, the result being tedious to navigate. A matrix like the one below facilitates identifying the value between any of the currencies:

The table needs to be multiplied by 12, the number of months, respectively by the number of years, and filter allowing to navigate the data as needed. For many operations is just needed to look use the EX for a given time division. There are however operations in which is needed to have a deeper understanding of one or more XR's evolution over time (e.g. GBP to NOK). 

Moreover, for some operations is enough to work with two decimals, while for others one needs to use up to 6 or even more decimals for each XR. Occasionally, one can compromise and use 3 decimals, which should be enough for most of the scenarios. Making sense of such numbers is not easy for most of us, especially when is needed to compare at first sight values across multiple columns. Summary tables can help:

Statistics like Min. (minimum), Max. (maximum), Max. - Min. (range), Avg. (average) or even StdDev. (standard deviation) can provide some basis for further analysis, while sparklines are ideal for showing trends over a time interval (e.g. months).

Usually, a heatmap helps to some degree to navigate the data, especially when there's a plot associated with it:

In this case filtering by column in the heatmap allows to see how an XR changed for the same month over the years, while the trendline allows to identify the overall tendency (which is sensitive to the number of years considered). Showing tendencies or patterns for the same month over several years complements the yearly perspective shown via sparklines.

Fortunately, there are techniques to reduce the representational complexity of such numbers. For example, one can use as basis the XRs for January (see Base Jan), and represent the other XRs only as differences from the respective XR. Thus, in the below table for February is shown the XR difference between February and January (13.32-13.22=0.10). The column for January is zero and could be omitted, though it can still be useful in further calculations (e.g. in the calculation of averages) based on the respective data..

This technique works when the variations are relatively small (e.g. the values vary around 0). The above plots show the respective differences for the whole year, respectively only for four months. Given a bigger sequence (e.g. 24, 28 months) one can attempt to use the same technique, though there's a point beyond which it becomes difficult to make sense of the results. One can also use the year end XR or even the yearly average for the same, though it adds unnecessary complexity to the calculations when the values for the whole year aren't available. 

Usually, it's recommended to show only 3-5 series in a plot, as one can better distinguish the trends. However, plotting all series allows to grasp the overall pattern, if any. Thus, in the first plot is not important to identify the individual series but to see their tendencies. The two perspectives can be aggregated into one plot obtained by applying different filtering. 

Of course, a similar perspective can be obtained by looking at the whole XRs:

The Max.-Min. and StdDev (standard deviation for population) between the last and previous tables must match. 

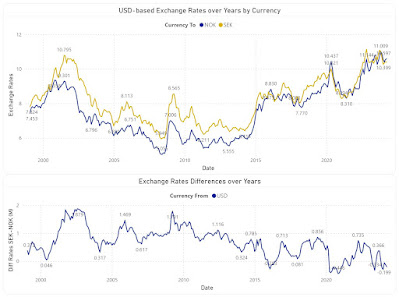
Certain operations require comparing the trends of two currencies. The first plot shows the evolution NOK and SEK in respect to EUR, while the second shows only the differences between the two XRs:

The first plot will show different values when performed against other currency (e.g. USD), however the second plot will look similarly, even if the points deviate slightly:

Another important difference is the one between monthly and yearly XRs, difference depicted by the below plot:

The value differences between the two XR types can have considerable impact on reporting. Therefore, one must reflect in analyses the rate type used in the actual process. 

Attempting to project data into the future can require complex techniques, however, sometimes is enough to highlight a probable area, which depends also on the confidence interval (e.g. 85%) and the forecast length (e.g. 10 months):

Every perspective into the data tends to provide something new that helps in sense-making. For some users the first table with flexible filtering (e.g. time unit, currency type, currency from/to) is enough, while for others multiple perspectives are needed. When possible, one should  allow users to explore the various perspectives and use the feedback to remove or even add more perspectives. Including a feedback loop in graphical representation is important not only for tailoring the visuals to users' needs but also for managing their expectations,  respectively of learning what works and what doesn't.

Comments:
1) I used GBP to NOK XRs to provide an example based on  triangulation.
2) Some experts advise against using borders or grid lines. Borders, as the name indicates allow to delimitate between various areas, while grid lines allow to make comparisons within a section without needing to sway between broader areas, adding thus precision to our senses-making. Choosing grey as color for the elements from the background minimizes the overhead for coping with more information while allowing to better use the available space.
3) Trend lines are recommended where the number of points is relatively small and only one series is involved, though, as always, there are exceptions too. 
4) In heatmaps one can use a gradient between two colors to show the tendencies of moving toward an extreme or another. One should avoid colors like red or green.
5) Ideally, a color should be used for only one encoding (e.g. one color for the same month across all graphics), though the more elements need to be encoded, the more difficult it becomes to respect this rule. The above graphics might slightly deviate from this as the purpose is to show a representation technique. 
6) In some graphics the XRs are displayed only with two decimals because currently the technique used (visual calculations) doesn't support formatting.
7) All the above graphical elements are based on a Power BI solution. Unfortunately, the tool has its representational limitations, especially when one wants to add additional information into the plots. 
8) Unfortunately, the daily XR values are not easily available from the same source. There are special scenarios for which a daily, hourly or even minute-based analysis is needed.
9) It's a good idea to validate the results against the similar results available on the web (see the ECB website).

Previous Post <<||>> Next Post

Data Management: Data Quality Dimensions (Part IV: Accuracy)

Data Management Series

Accuracy refers to the extent data is correct, matching the reality with an acceptable level of approximation. Correctness, the value of being correct, same as reality are vague terms, in many cases they are a question of philosophy, perception, having a high degree of interpretability. However, in what concerns data they are typically the result of measurement, therefore a measurement of accuracy relates to the degree the data deviate from physical laws, logics or defined rules, though also this context is a swampy field because, utilizing a well-known syntagm, everything is relative. 

From a scientific point of view, we try to model the reality with mathematical models which offer various level of approximation, the more we learn about our world, the more flaws we discover in the existing models, it’s a continuous quest for finding better models that approximate the reality. Things don’t have to be so complicated, for basic measurements there are many tools out there that offer acceptable results for most of the requirements, on the other side, as requirements change, better approximations might be required with time.

Another concept related with the ones of accuracy and measurement systems is the one of precision, and it refers to degree repeated measurements under unchanged conditions lead to the same results, further concepts associated with it being the ones of repeatability and reproducibility. Even if the accuracy and precision concepts are often confounded a measurement system can be accurate but not precise or precise but not accurate (see the target analogy), a valid measurement system targeting thus both aspects. Accuracy and precision can be considered dimensions of correctedness.

Coming back to accuracy and its use in determining data quality, typically accuracy it’s strong related to the measurement tools used, for this being needed to do again the measurements for all or a sample of the dataset and identify whether the requested level of accuracy is met, approach that could involve quite an effort. The accuracy depends also on whether the systems used to store the data are designed to store the data at the requested level of accuracy, fact reflected by the characteristics of data types used (e.g. precision, length).

Given the fact that a system stores related data (e.g. weight, height, width, length) that could satisfy physical, business of common-sense rules could be used rules to check whether the data satisfy them with the desired level of approximation. For example, being known the height, width, length and the composition of a material (e.g. metal bar) could be determined the approximated weight and compared with entered weight, if the difference is not inside of a certain interval then most probably one of the values were incorrect entered. There are even simpler rules that might apply, for example the physical dimensions must be positive real values, or in a generalized formulation - involve maximal or minimal limits that lead to identification of outliers, etc. In fact, most of the time determining data accuracy resumes only at defining possible value intervals, though there will be also cases in which for this purpose are built complex models and specific techniques.

There is another important aspect related to accuracy, time dependency of data – whether the data changes or not with time. Data currency or actuality refers to the extent data are actual. Given the above definition for accuracy, currency could be considered as a special type of accuracy because when the data are not actual then they don’t reflect reality. If currency is considered as a standalone data quality dimension, then accuracy refers only to the data that are not time dependent.

Previous Post <<||>> Next Post

Written: Jan-2010, Last Reviewed: Mar-2024