🕸Systems Engineering: Never-Ending Stories in Praxis (Quote of the Day)

Systems Engineering Cycle

"[…] the longer one works on […] a project without actually concluding it, the more remote the expected completion date becomes. Is this really such a perplexing paradox? No, on the contrary: human experience, all-too-familiar human experience, suggests that in fact many tasks suffer from similar runaway completion times. In short, such jobs either get done soon or they never get done. It is surprising, though, that this common conundrum can be modeled so simply by a self-similar power law." (Manfred Schroeder, "Fractals, Chaos, Power Laws Minutes from an Infinite Paradise", 1990)

I found the above quote while browsing through Manfred Schroeder's book on fractals, chaos and power laws, book that also explores similar topics like percolation, recursion, randomness, self-similarity, determinism, etc. Unfortunately, when one goes beyond the introductory notes of each chapter, the subjects require more advanced knowledge of Mathematics, respectively further analysis and exploration of the models behind. Despite this, the book is still an interesting read with ideas to ponder upon.

I found myself a few times in the situation described above - working on a task that didn't seem to end, despite investing more effort, respectively approaching the solution from different angles. The reasons residing behind such situations were multiple, found typically beyond my direct area of influence and/or decision. In a systemic setup, there are parts of a system that find themselves in opposition, different forces pulling in distinct directions. It can be the case of interests, goals, expectations or solutions which compete or make subject to politics. 

For example, in Data Analytics or Data Science there are high chances that no progress can be made beyond a certain point without addressing first the quality of data or design/architectural issues. The integrations between applications, data migrations and other solutions which heavily rely on data are sensitive to data quality and architecture's reliability. As long the source of variability (data, data generators) is not stabilized, providing a stable solution has low chances of success, no matter how much effort is invested, respectively how performant the tools are. 

Some of the issues can be solved by allocating resources to handle their implications. Unfortunately, some organizations attempt to solve such issues by allocating the resources in the wrong areas or by addressing the symptoms instead of taking a step back and looking systemically at the problem, analyzing and modeling it accordingly. Moreover, there are organizations which refuse to recognize they have a problem at all! In the blame game, it's much easier to shift the responsibility on somebody else's shoulders. 

Defining the right problem to solve might prove more challenging than expected and usually this requires several iterations in which the knowledge obtained in the process is incorporated gradually. Other times, one attempts to solve the correct problem by using the wrong methodology, architecture and/or skillset. The difference between right and wrong depends on the context, and even between similar problems and factors the context can make a considerable difference.

The above quote can be corroborated with situations in which perfection is demanded. In IT and management setups, excellence is often confounded with perfection, the latter being impossible to achieve, though many managers take it as the norm. There's a critical point above which the effort invested outweighs solution's plausibility by an exponential factor.  

Another source for unending effort is when requirements change frequently in a swift manner - e.g. the rate with which changes occur outweighs the progress made for finding a solution. Unless the requirements are stabilized, the effort spirals towards the outside (in an exponential manner). 

Finally, there are cases with extreme character, in which for example the complexity of the task outweighs the skillset and/or the number of resources available. Moreover, there are problems which accept plausible solutions, though there are also problems (especially systemic ones) which don't have stable or plausible solutions. 

Behind most of such cases lie factors that tend to have chaotic behavior that occurs especially when the environments are far from favorable. The models used to depict such relations are nonlinear, sometimes expressed as power laws - one quantity varying as a power of another, with the variation increasing with each generation. 

Previous Post <<||>> Next Post

Resources:
[1] Manfred Schroeder, "Fractals, Chaos, Power Laws Minutes from an Infinite Paradise", 1990 (quotes)

💠🛠️🛠️🗒️SQL Server: Buffer Pool [Notes]

Disclaimer: This is work in progress intended to consolidate information from various sources (some unfortunately not available anymore).

Buffer Pool  [aka BP, BPool]

• main memory component in SQL Server [2]
• ⇐ preferred memory allocator for the whole server [1]
• ⇐ the biggest consumer of SQL Server 
• area of memory that SQL Server used to store
• cached data (aka data pages)
• cached execution plans 
• algebrizer trees for views, constraints and defaults
• lock memory
• ⇐ anything with a non-zero value in sys.dm_os_memory_clerks.single_pages_kb
• ⇐ caching data in the buffer pool reduces the load on the I/O subsystem and improves performance [6]
• ⇐ all pages must be copied into the buffer pool before they can be used in a query
•  ⇒ it is needed to scan the buffer pool for a number of operations [3]
• single-page allocator
• it commits and decommits memory blocks of 8KB granularity only
• manages disk I/O functions for bringing data and index pages into the data cache so data can be shared among users [2]
• all memory not used by another memory component remains in the buffer pool to be used as a data cache for pages read in from the database files on disk [2]
• when other components require memory, they can request a buffer from the buffer pool [2]
• most of the buffers taken from the buffer pool for other memory components go to other kinds of memory caches [2]
• ⇐ they can only get blocks of 8KB in size [1]
• these blocks are not continues in memory[1]
• allocation for large buffers will be satisfied by memory node's multi-page allocator or by virtual allocator [1]
• ⇒ memory will be allocated outside of Buffer Pool [1]
• BP can be used as underneath memory manager for SQL Server components as long as they allocate buffers of 8KB [1]
• pages allocated from BP are referred as stolen[1]
• first decides how much of VAS it needs to reserve for its usage (aka target memory)
• decision based on internal memory requirements and external memory state
• it calculates its target amount of memory it thinks it should commit before it can get into memory pressure [1]
• ⇐ to keep the system out of paging the target memory is constantly recalculated [1]
• {restriction} the target memory can't exceed max memory that represents max server memory settings [1]
• even if the min server memory equals the max server memory BP commits its memory on demand [1]
• ⇐ monitor the corresponding profiler event to observe this behavior [1]
• reserves all of it right a way
• ⇐ check monitor SQL Server's virtual bytes from perfmon or use vasummary view to observe this behavior 
• ⇐ normally can't get all the needed memory in one region
• ⇒ several large regions reserved ← by design behavior 
• commits pages on demand
• during startup the memory manager configures BP to be SQLOS's single page allocator
• from that point on all dynamic single page allocations are provided by BP[1]
• has its own memory clerk
• is leveraged to respond to external and VAS memory pressure only [47]
• leverages only Virtual and AWE SQLOS's interfaces
• never uses any type of page allocator from SQLOS [1]
• {operation} dropping buffers 
• likely results in some degree of performance degradation
• ⇐ any subsequent query executions will have to reread the data from the database files increasing I/O
• via: DBCC DROPCLEANBUFFERS
• {concept} page
• the fundamental unit of data storage in SQL Server
• {concept} buffer
• page in memory that's the same size as a data or index page [2]
• ⇐ page frame that can hold one page from a database [2]
• {concept} buffer pool scan
• common internal operation that iterates through the entire buffer descriptor array to find any buffers that belong to a specific database [3]
• [<SQL Server 2022] serial operation
• on large memory machines operations that require scanning the buffer pool can be slow [3]
• ⇐ the larger the machine, the greater the impact 
• ⇐ it doesn’t necessarily matter about the size of the operation [3]
• [SQL Server 2022] {feature}Buffer Pool Parallel Scan
• parallelized by utilizing multiple cores
• adds processing power to scan the buffer pool more efficiently [3]
• ⇐ benefits both small and large database operations on larger memory machines
• 10-30x improvement in executions
• customers running mission-critical OLTP, hosted service providers, and data warehouse environments will witness the most improvements in overall processing speed [3]
• uses one task per 8 million buffers (64 GB) 
• ⇐ a serial scan will still be used if there are less than 8 million buffers [3]
• uses buffer pool scan diagnostics to improve supportability and insights with new buffer pool scan events [3]
• can significantly improve the performance of database workloads
• operations benefiting from it
• database startup/shutdown
• creating a new database
• file drop operations
• backup/restore operations
• Always On failover events
• DBCC CHECKDB and DBCC Check Table
• log restore operations
• other internal operations (e.g., checkpoint) 

Previous Post <<||>>  Next Post

References:
[1] Slava Oaks (2005) SQLOS's memory manager and SQL Server's Buffer Pool (link) [something similar seems to be available here]
[2] Kalen Delaney (2006) Inside Microsoft® SQL Server™ 2005: The Storage Engine
[3] Microsoft SQL Server Blog (2022) Improve scalability with Buffer Pool Parallel Scan in SQL Server 2022, by David Pless (link)
[4] Microsoft learn (2022) Operations that trigger a buffer pool scan may run slowly on large-memory computers (link)

[5] Microsoft Docs (2023) DBCC TRACEON - Trace Flags (link)

[6] Dmitri Korotkevitch (2015) Expert SQL Server: In-Memory OLTP

[7] Slava Oaks (2005) SQLOS's memory manager: responding to memory pressure (link)

💫ERP Systems: Microsoft Dynamics 365's Invoice Capture (Features)

Disclaimer: This is work in progress intended to consolidate information from the various sources (what I considered as important during my exploration of the documentation and further communication) and not to provide an overview of all the features. Please refer to the documentation for a complete overview!

In what concerns the releases see [2].
Last updated: 23-May-2024

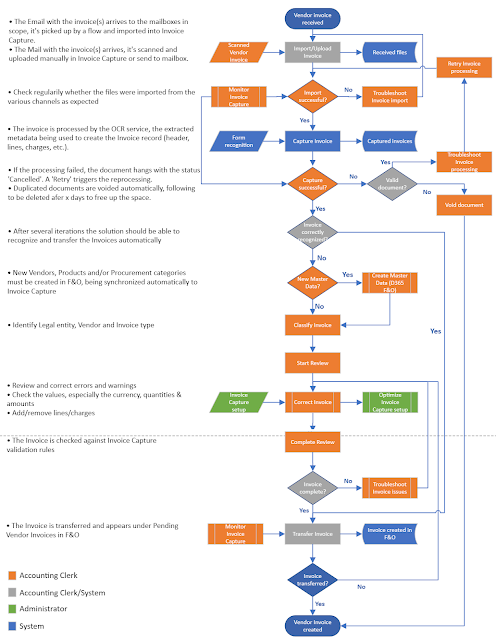
Invoice Capture - Main Components [3]

AI Model

• {feature} prebuilt model (aka Invoice processing model) [by design]
• can handle the most common invoices in various languages
• owned by Microsoft and cannot be trained by the customers
• {feature} custom prebuilt models [planned]
• built on top of the prebuilt model to handle more complex invoice layouts
• only requires to train the exceptional invoices
• after a model is published, additional mapping is required to map the model fields to the invoice files
• {feature} custom model [by design]
• requires training the model from scratch 
• costs time and effort
• supports the Charges and Sales Tax Amount fields [1.5.0.2]
• support lookup lists on custom fields [1.6.0.x]

Channels

• flows that collect the invoices into one location 
• there's always a 1:1 relationship between flows and channels
• multiple channels can be defined using different triggers based on Power Automated connectors
• {feature}default channel for Upload files [1.0.1.0]
• {feature} supports multiple sources via flow templates [by design]
• Outlook.com
• Microsoft Outlook 365
• Microsoft Outlook 365 shared mailbox [1.1.0.10]
• to achieve similar behavior one had to modify the first steps of the generated flow with the "When a new email arrives in a shared mailbox (V2)" trigger
• SharePoint
• OneDrive
• OneDrive for business [1.0.1.0]
• {feature} assign legal entity on the channel
• the LE value is automatically assigned without applying additional derivation logic [1]
• invoices sent via predefined channels are captured and appear on the 'Received files' page

Configuration groups 

• allow managing the list of invoice fields and the manual review settings 
• can be assigned for each LE or Vendors. 
• all the legal entities in the same configuration group use the same invoice fields and manual review setting
• default configuration group 
• created after deployment, can't be changed or deleted
• 
  

Fields

• {feature} standard fields 
• Legal entity 
• organizations registered with legal authorities in D365 F&O and selected for Invoice capture
• {feature} allow to enforce role-based security model
• {feature} synchronized from D365 F&O to CRM 
• {missing feature} split the invoices between multiple LEs
• Vendor master 
• individuals or organizations that supply goods or services
• used to automatically derive the Vendor account
• {feature} synchronized from D365 F&O to CRM
• synchronization issues solved [1.6.0.x]
• {feature}Vendor account can be derived from tax number [1.0.1.0]
• Invoice header
• {feature} Currency code can be derived from the currency symbol [1.0.1.0]
• Invoice lines
• Item master
• {feature} Item number can be derived from External item number [1.0.1.0]
• {feature} default the item description for procurement category item by the value from original document [1.1.0.32/10.0.39]
• Expense types (aka Procurement categories) 
• Charges
• amounts added to the lines or header
• {feature} header-level charges [1.1.0.10]
• {missing feature}line-level charges 
• {feature}Financial dimensions 
• header level [1.1.0.32/10.0.39]
• line level [1.3.0.x]
• Purchase orders
• {feature} PO formatting based on the number sequence settings
• {missing feature}PO details
• {missing feature} multiple POs, multiple receipts 
• {missing feature} Project information integration
• {workaround} the Project Id can be added as custom field on Invoice line for Cost invoices and with this the field should be mapped with the corresponding Data entity for transferring the value for D365 F&O
• {feature} custom fields [1.1.0.32/10.0.39]

File filter

• applies additional filtering to incoming files at the application level
• with the installation a default updatable global file filter is provided
• can be applied at different channel levels
• {event} an invoice document is received
• the channel is checked first for a file filter
• if no file filter is assigned to the channel level, the file filter at the system level is used [1]
• {configuration} maximum files size; 20 MB
• {configuration} supported files types: PDF, PNG, JPG, JPEG, TIF, TIFF
• {configuration} supported file names 
• filter out files that aren't relevant to invoices [1]
• rules can be applied to accept/exclude files whose name contains predefined strings [1]

Actions 

• Import Invoice
• {feature} Channel for file upload
• a default channel is provided for directly uploading the invoice files
• maximum 20 files can be uploaded simultaneously
• Capture Invoice
• {feature} Invoice capture processing
• different derivation rules are applied to ensure that the invoices are complete and correct [1]
• {missing feature} differentiate between relevant and non-relevant content}
• {missing feature} merging/splitting files
• {workaround} export the file(s), merge/split them, and import the result
• Void files [1.0.1.0]
• once the files voided, it is allowed to be deleted from Dataverse
• saves storage costs
• Classify Invoice
• {feature} search for LEs
• {feature} assign LE to Channel
• AP clerks view only the invoices under the LE which are assigned to them
• {feature} search for Vendor accounts by name or address 
• Maintaining Headers
• {feature} multiple sales taxes [1.1.0.26]
• {missing feature} rounding-off [only in D365 F&O]
• {feature} support Credit Notes [1.5.0.2]
• Maintaining Lines
• {feature} Add/remove lines
• {feature} "Remove all" option for deleting all the invoice lines in Side-by-Side Viewer [1.1.0.26]
• Previously it was possible to delete the lines one by one, which by incorrectly formatted big invoices would lead to considerable effort. Imagine the invoices from Microsoft or other cloud providers that contain 5-10 pages of lines. 
• {feature}Aggregate multiple lines [requested]
• Now all lines from an invoice have the same importance. Especially by big invoices, it would be useful to aggregate the amounts from multiple lines under one. 
• {feature} Show the total amount across the lines [requested]
• When removing/adding lines, it would be useful to compare the total amount across the lines with the one from the header. 
• Check the UoM consistency between invoice line and linked purchase order line
• For the Invoice to be correctly processed, the two values must match. 
• Support for discounts [requested]
• as workaround, discounts can be entered as separate lines
• Transfer invoice
• 
  
• Automation
• {parameter} Auto invoice cleanup
•  automatically cleans up the transferred invoices and voided invoices older than 180 days every day [1]
• Use continuous learning 
• select this option to turn on the continuous learning feature
• learns from the corrections made by the AP clerk on a previous instance of the same invoice [1]
• records the mapping relationship between the invoice context and the derived entities [1]
• the entities are automatically derived for the next time a similar invoice is captured [1]
• {missing feature} standard way to copy the continuous learning from UAT to PROD
• {feature} migration tool for continuous learning knowledge
• allows us to transfer the learning knowledge from one environment to another [1.6.0.x]
• Confidence score check
• for the prebuilt model the confidence score is always the same 
• its value is returned by the AI Builder service
• confidence score can only be improved only when the customer prebuilt model is used 
•  it can be increased by uploading more samples and do the tagging accordingly
• a low confidence score is caused by the fact that not enough samples with the same pattern have been trained
• {parameter} control the confidence score check [1.1.0.32/10.0.39]
• Manage file filters

User Interface

• Side-by-side view [by design]
• 
  
• History logs [1.0.1.0]
• supported in Received files and Captured invoices
• help AP clerks know the actions and results in each step during invoice processing 
• Navigation to D365 F&O [1.0.1.0]
• once the invoice is successfully transferred to D365 F&O, a quick link is provided for the AP clerk to open the Pending vendor invoice list in F&O
• Reporting
• {missing feature} consolidated overview across multiple environments (e.g. for licensing needs evaluation)
• {missing features} metrics by Legal entity, Processing status, Vendor and/or Invoice type
• {workaround} a paginated report can be built based on Dataverse

Data Validation

• [Invoice Capture] derivation rules 
• applied to ensure that the invoices are complete and correct [1]
• {missing feature} derive vendor using the associated email address
• {parameter} Format purchase order 
• used to check the number sequence settings in D365 F&O to format the PO number [1]
• {parameter} Derive currency code for cost invoice
• used to derive the value from invoice master data in D365 F&O [1]
• <-- the currency code on PO Invoices must be identical to the one on PO
• {parameter} Validate total sales tax amount 
• validates the consistency between the sales tax amount on the Sales tax card and the total sales tax amount, when there's a sales tax line [1]
• {parameter} Validate total amount 
• confirm alignment between the calculated total invoice amount and the captured total amount [1]
• [D365 F&O] before workflow submissions [requested]
• it makes sense to have out-of-box rules 
• currently this can be done by implementing extensions
• [D365 F&O] during workflow execution [by design]

Dynamics 365 for Finance [aka D365 F&O]

• Attachments 
• {parameter} control document type for persisting the invoice attachment in D365 F&O [1.1.0.32/10.0.39]
• Invoice Capture
• {parameter} select the entities in scope
• {parameter}differentiate by Invoice type whether Vendor invoice or Invoice journal is used to book the invoices
• {parameter} Transfer attachment
• Fixed Assets
• {missing feature} create Fixed asset automatically during the time the invoice is imported
• Vendor Invoice Journal 
• {missing feature} configure what journal the invoice is sent to
• the system seems to pick the first journal available
• {parameter} control journal name for creating 'Invoice journal'  [1.1.0.32/10.0.39]
• {missing feature}grouping multiple invoices together in a journal (e.g., vendor group, payment terms, payment of method)
•  Approval Workflow
• {missing feature} involve Responsible person for the Vendor [requested]
• {missing feature} involve Buyer for Cost invoices [requested]
• {missing feature} differentiator between the various types of invoices [requested]
• {missing feature} amount-based approval [requested]
• Billing schedule
• {feature} integration with Billing schedules
• {feature} modify or cancel Billing schedules
• Reporting
• {missing feature} Vendor invoices hanging in the approval workflow (incl. responsible person for current action, respectively error message)
• {missing feature} Report for GL reconciliation between Vendor invoice and GL via Billing schedules
• {missing feature} Overview of the financial dimensions used (to identify whether further setup is needed)

Previous post <<||>> Next post

Resources:
[1] Microsoft Learn (2023) Invoice capture overview (link)
[2] Yammer (2023) Invoice Capture for Dynamics 365 Finance (link)
[3] Microsoft (2023) Invoice Capture for Dynamics 365 Finance - Implementation Guide

Acronyms:
AI - Artificial Intelligence 
AP - Accounts Payable
F&O - Finance & Operations
LE - Legal Entity
PO - Purchase Order
UoM- Unit of Measure

💫ERP Systems: Microsoft Dynamics 365's Vendor Invoices Processing (Setup Areas)

ERP Systems

Invoices can be set up to be imported automatically in Dynamics 365 for Finance and Operation (D365 F&O) via Invoice Capture (see process). Besides the Invoice Capture-related set up, there are several areas related to Vendor invoice's processing:

General Ledger

Accounts for automatic transactions need to be defined at least for the 'Vendor invoice rounding off' and 'Rounding variance', respectively for the 'Exchange rate gain' and 'Exchange rate loss', if this wasn't done already.

To facilitate accounts' reconciliation and reporting, one can enable a Batch transfer rule for the Source document type 'Vendor invoice' and thus one journal is used for each Vendor invoice. This also makes sure that the Description from Invoice will be taken over in the Journal, which facilitates accounts' reconciliation.

Subscription Billing

In case one needs to defer the amounts over a time interval (e.g. x months), as it's the case for prepayments, the integration with Subscription Billing on the Vendor side in F&O seems to work with minimal configuration. A Billing schedule is created for each Invoice distribution and can be modified or cancelled after the Invoice is posted, if needed.

If your organization uses Subscription Billing also for Accounts Receivables (AR), one might need to compromise on the setup because the same parameters are used for both modules. 

In what concerns accounts' reconciliation, there seems to be a 1:1 mapping between the Schedule line and the General Ledger (GL) posting, a table with the mapping between the records being available. One can build thus a Paginated report to display the mapping between AP and GL, if the infrastructure is in place (e.g. by building a data lakehouse/warehouse based on F&O, see post). 

Fixed Assets

One can enable the creation of Fixed assets by checking the "Create asset during product receipt or invoice posting" radio button in Fixed assets parameters.

The feature "create the fixed asset automatically during the time of invoice import" for PO-based Invoices (with "Create Fixed Asset" flag set at line level) doesn't seem to be supported yet.

Vendor Invoice Journals

Before Invoice Capture, Vendor invoice journals were helpful for posting summarized cost invoices that are not associated with POs (e.g. expenses for supplies or services). One can still use this approach, however if the line-based details are important, then it makes sense to use Pending vendor invoice with Service items or Procurement categories.  

A single Vendor invoice is created as one Vendor invoice journal. 

Organization Administration

When using workflows, setting the same language for all LEs can reduce the amount of redundant information maintained in the workflow(s), otherwise the texts need to be provided for each language. 

Default descriptions can be enabled for Purchase orders' invoice ledger and vendor to carry the same description entered Pending Vendor Invoices in Invoices and Journals. The functionality works also for Cost invoices.

Ideally, Invoice's description should have been maintained in Invoice capture and/or Microsoft should have provided a default description also for it. 

System

Unless there's a requirement to post manually the journals from subledger to GL, a batch transfer for subledger journals must be created for each LE.

One can enable email notifications for the users participating in workflows and use workflow delegations for the intervals the respective users are on leave. 

All users participating in the workflow must be available also as active employees. It makes sense to do latest when the integration goes Live. Moreover, the Users need to have the appropriate permissions for the roles they have in the process.

Vendor Invoice Automation

There's further functionality available under the 'Vendor Invoice Automation' label (see [1], [2]), though the following are the most important ones: 

• Automatically apply prepayments to vendor invoices
• Automatically submit imported invoices to the workflow system.
• Match product receipts to pending vendor invoice lines.

Recurring Vendor Invoice Templates

Microsoft introduced with 10.0.38 PU a new feature called 'Vendor invoice templates', which allows creating recurring vendor invoices without the need to enter all the vendor invoice information for each separate invoice (see [3]). There seems to be no information available whether any integration between this feature and Invoice Capture will be supported.

E-Invoicing

EU countries need to enforce the Directive 2014/55/EU for Vendor and Customer invoices. The directive requires that the electronic exchange of invoice documents between suppliers and buyers to occur over government-held third-party solutions. Each country has its own system(s) and regulations with different scope and timelines. Some countries have already requirements for 2024, respectively 2025 and there are similar projects in US and other countries. 

Even if Microsoft started this year (2023) to provide country-specific integrations for e-Invoicing, for the moment there seem no information available on how e-Invoicing will integrate with Invoice Capture.

Previous post <<||>> Next post

Resources:
[1] Microsoft Learn (2023) Vendor Invoice Automation (link)
[2]Microsoft Dynamics 365 (2023) The Future of Finance: Unlocking the Benefits of Accounts Payable Automation (link)
[3] Hylke Britstra (2023) Recurring vendor invoice templates (link)
[4] Dan Edwards (2023) AP Automation at DynamicsCon (link)

💫ERP Systems: Microsoft Dynamics 365's Invoice Capture (Setup Areas)

ERP Systems

When implementing the Invoice Capture process, there are several setup areas that need to be considered into the Power App (Channels & Mapping Rules), some that need to be done in Dynamics 365 for Finance and Operations (D365 F&O) and impact the integration with the Power App (Expense types/Procurement categories, Financial dimensions, Approval workflow), respectively setup that concerns only D365 F&O but still important. In addition, there are also overlapping features like Recurring Vendor Invoice Templates and E-Invoicing.

This post focuses on the first two types of setup areas, the rest following  in a second post. 

Channels

In the digitalization era, it's expected that most of the Vendor invoices are received by email or an integrated way (see e-Invoicing). However there can be also several exceptions (e.g. small companies operating mostly offline).

In Invoice Capture can be defined one or more channels for Outlook, SharePoint or OneDrive on which Invoices can be imported in the App. In a common scenario, depending on the number of mailboxes intended for use, one or more channels can be set up for Outlook. Power App listens on the respective channels for incoming emails in the Inbox, in a first step processes the emails by importing all the attachments (including signature images), while in a second step processes all the documents that look like an Invoice (including Receipts) and extracts the metadata to create the Invoice record. The Invoices received in hard-paper format can be scanned and sent to one of the internal mailboxes, respectively imported manually in Invoice Capture. 

More likely, there will be also a backlog that can be imported via SharePoint or OneDrive, which is more convenient than resending the backlog by email. In the end it should make no difference for the process which channels is used as long as the Invoices are processed in a timely manner. It should make also no difference if for example in UAT were used other channels than in Production. For testing purposes it might be advantageous to have more control over which Invoices are processed, while the UAT could follow the same setup as Prod, which is generally recommended.

Mapping Rules

The mapping rules allow on one side to set default values based on a matching string checked against several attributes (e.g. Company name, Address or Tax registration number for Legal entity, Item number for Item, Item description for Expense type). Secondly, they allow to also define a configuration for a rule, which defines what fields are mandatory, respectively which Invoice types are supported, etc.

The mapping rules will not cover all scenarios, though it's enough if they cover a good percentage from the most common cases. Therefore, over time they are also good candidates for further optimization. Moreover, because Invoice Capture remembers the values used before for an instance of the same Invoice, the mapping rules will be considered only for the first occurrence of the respective Invoice or whatever is new in its processing. 

If a channel was defined for each Legal entity, this seems to make obsolete the definition of mapping rules for it. Conversely, if the number of manual uploads is not neglectable, it still makes sense to define a mapping rule. 

Mapping rules for the Expense type seem to work well when Items' descriptions are general enough to include certain words (e.g. licenses, utilities). 

One can define mapping rules also for the Vendor accounts and Items, though it's questionable whether the effort makes sense as long as the internal Vendor names and Product numbers don't deviate from the ones used by the Vendor itself.

Expense Types

Invoice Capture requires that either the Item or the Expense type are provided on the line. For PO-based invoices, an Item should be available. Cost invoices can have Items as well and they can be used on the line, though from the point of view of the setup it might be easier to use Expense types. It's the question whether the information loss has any major impact on the business. There are also cases in which the lines don't bring any benefit and can be thus in Invoice capture deleted. 

At least for Cost invoices, the Expense types (aka Procurement categories in Dynamics 365) defined can considerably facilitate the automatic processing. D365 F&O can use the Procurement category to automatically populate the Main Account in the Invoice distributions. The value is used as default and can be overwritten, if needed. 

Having for example a 1:1 mapping between Procurement categories and Main accounts, respectively the same names can make easier the work of AP Clerks and facilitate the troubleshooting.

Conversely, one can define an additional level of detail (aka an additional segment) for reporting purposes. This implies that multiple categories will point to the same Main account, which can increase the overhead, though the complexity of the structure can be simplified by using maybe a good naming convention and a consolidated Excel list with the values. The overhead resumes mainly when dealing with the first instance of an Vendor invoice.

On Procurement categories can be defined also the default Item sales tax groups (a 1:1 mapping) which can be overwritten as well. For the categories with multiple Items sales tax groups, one should decide whether the benefit of providing a default value outweighs the effort for adding the value for each Invoice line. 

Defining upfront, before the Go Live, a good hierarchical structure for the Procurement categories and the mappings to the Main accounts, respectively to the Item sales tax groups can reduce the effort of maintaining the structure later and reduces the reporting overhead. 

Financial Dimensions & the Vendor Invoice Approval Workflow

Besides their general use, the Financial dimensions can be used to implement an approval process on D365 F&O side by configuring an expenditure reviewer (see [2]) and using it in the Vendor Invoice Approval workflow, respectively of setting up the financial owners for each dimension in scope. Different owners for the Financial dimensions can be defined for each Legal entity via Legal entity overrides. From what it seems, notifications are sent then to the override as well to the default owner. 

Starting with the 1.1.0.32 (07-Nov-2023) version of Invoice capture, respectively the 10.0.39 version of D365 F&O (planned for Apr-2024), 3 financial dimensions (Cost center, Department and Legal Entity) are supported directly in the App. This would allow us to cover the example covered in [2]). This reduces the need for maintaining the values in D365 F&O. 

Unfortunately, if the approval process needs to use further dimensions (e.g. Vendor, Location) or attributes (e.g. Invoice responsible person) in the approval, one needs either to compromise or find workarounds. If there's no Purchase order as in the case of Cost invoices, involving the actual Buyer is almost impossible. For such extreme cases one needs more flexibility in the approval process and hopefully Microsoft will extend the functionality behind it.

The approval processes needed by customers require occasionally a complexity that's not achievable with the functionality available in D365 for F&O. The customers are forced then either to compromise or use external tools (e.g. Power Automate) for building the respective functionality. 

One should consider defining default Financial dimensions on the Vendor, the respective values being used when generating the Invoice in D365 F&O. Defining Financial dimensions templates can help as well when the costs need to be split across different Financial dimensions based on percentages. 

In case the financial dimensions differ across a same Vendor's invoices, one can request from the Vendors to provide the respective information on the Invoice. 

Organization Administration

Cost invoices can work without providing a Unit of Measure (UoM) in Invoice capture, however one should consider using an UoM at least for aesthetic purposes in reporting. On the other side, this can complicate the setup if the same UoM is used for other purposes. 

Vendor Invoice Automation

To be able to process automatically the Vendor invoices once they arrived in D365 F&O, it would useful to maintain the attributes which are modified manually in D365 F&O directly in Invoice Capture. The usual fields are the following:

• Invoice description (header)
• Financial dimensions 
• Sales item tax group

Master Data Management

There are master data attributes which even if they are not directly involved in the process, they could make process actor's life a bit easier. It can be the case of the Responsible person and/or the Buyer group, which would allow the AP Clerks to identify the Cost Center and Department related to the Invoice. Maintaining the external Item descriptions for Vendors can help as well in certain scenarios. 

Previous post <<||>> Next post

Resources:
[1] Microsoft Learn (2023) Invoice capture overview (link)
[2] Microsoft Learn (2023) Configure expenditure reviewers (link)

💎SQL Reloaded: Blocked Products in Dynamics 365 F&O

Besides listing the products released by Legal entity (see previous post), it's useful to know whether they were blocked for Inventory, Sales or Procurement. This is quite easy when doing it over the data entity:

-- check status via the data entity
SELECT PSO.ItemNumber 
, PSO.DataAreaId 
, PSO.IsSalesProcessingStopped
, PSO.IsInventoryProcessingStopped 
, PSO.IsProcurementProcessingStopped
FROM dbo.InventProductSpecificOrderSettingsV3Entity PSO
ORDER BY PSO.ItemNumber 
, PSO.DataAreaId

However, when the data entity is not available, the logic gets a bit more complex because the data are stored in 3 different tables: InventItemInventSetup, InventItemPurchSetup, respectively InventItemSalesSetup. Here's the piece of logic used to get the various statuses in AX 2009 (of course, without the JOINs on Partition) and it works also in Dynamics 365 F&O:

/* Product Specific Order Settings via JOINs */
SELECT ITM.DataAreaId 
, ITM.ItemId 
, IPS.Stopped IsProcurementProcessingStopped
, ILS.Stopped IsInventoryProcessingStopped
, ISS.Stopped IsSalesProcessingStopped
FROM dbo.InventTable ITM
     LEFT JOIN dbo.InventItemPurchSetup IPS

       ON ITM.ItemID = IPS.ItemId
      AND ITM.DataAreaId = IPS.DataAreaId 
      AND ITM.Partition = IPS.Partition
      AND IPS.InventDimId = 'AllBlank'
     LEFT JOIN dbo.InventItemSalesSetup ISS
       ON ITM.ItemID = ISS.ItemId
      AND ITM.DataAreaId = ISS.DataAreaId 
      AND ITM.Partition = ISS.Partition
      AND ISS.InventDimId = 'AllBlank'
     LEFT JOIN dbo.InventItemInventSetup ILS
       ON ITM.ItemID = ILS.ItemId
      AND ITM.DataAreaId = ILS.DataAreaId 
      AND ITM.Partition = ILS.Partition
      AND ILS.InventDimId = 'AllBlank'
ORDER BY ITM.ItemId
,  ITM.DataAreaId 

The constraint on InventDimId is necessary because there can be multiple records for the Product and Legal entity combination. 

Alternatively, one can use UNIONs instead of JOINs and include the logic into a view to simplify the final query (the query was written to test the behavior in a distributed environment like serverless SQL pool):

-- create the view
CREATE OR ALTER VIEW TDM.vProductSpecificOrderSettings
AS
/* Product Specific Order Settings via UNIONs */
SELECT IST.DataAreaId 
, IST.ItemId 
, IST.Partition 
, max(IST.IsInventoryProcessingStopped) IsInventoryProcessingStopped
, max(IST.IsSalesProcessingStopped) IsSalesProcessingStopped
, max(IST.IsProcurementProcessingStopped) IsProcurementProcessingStopped
FROM (
	-- inventory
	SELECT IIS.DataAreaId 
	, IIS.ItemId 
	, IIS.Partition
	, IIS.Stopped IsInventoryProcessingStopped
	, 0 IsSalesProcessingStopped
	, 0 IsProcurementProcessingStopped
	FROM dbo.InventItemInventSetup IIS
	WHERE IIS.InventDimId = 'AllBlank'
	UNION ALL
	-- purchasing
	SELECT IPS.DataAreaId 
	, IPS.ItemId 
	, IPS.Partition 
	, 0
	, 0
	, IPS.Stopped
	FROM dbo.InventItemPurchSetup IPS
	WHERE IPS.InventDimId = 'AllBlank'
	UNION ALL
	-- sales
	SELECT ISS.DataAreaId 
	, ISS.ItemId 
	, ISS.Partition 
	, 0
	, ISS.Stopped
	, 0
	FROM dbo.InventItemSalesSetup ISS
	WHERE ISS.InventDimId = 'AllBlank'
 ) IST
 GROUP BY IST.DataAreaId 
, IST.ItemId 
, IST.Partition 

/* Product Specific Order Settings via UNIONs */
SELECT ITM.DataAreaId 
, ITM.ItemId 
, PSO.IsInventoryProcessingStopped
, PSO.IsSalesProcessingStopped
, PSO.IsProcurementProcessingStopped
FROM dbo.InventTable ITM
     LEFT JOIN TDM.vProductSpecificOrderSettings PSO
	   ON ITM.ItemId = PSO.ItemId 
	  AND ITM.DataAreaId = PSO.DataAreaId 
	  AND ITM.Partition = PSO.Partition
ORDER BY ITM.ItemId 
, ITM.DataAreaId 

At least for the database used for testing on an SQL Server 2022 instance, the last query has slightly lower estimated subtree cost and memory grant than the previous one. It's also interesting that the data entity-based query outperforms the other two queries. 

And here's the combined query from this and previous post:

-- Legal Entities vs Products incl. product order settings
SELECT DAT.Id DataAreaId 
, PRD.DisplayProductNumber ItemId 
, CASE WHEN ITM.DataAreaId IS NOT NULL THEN 1 ELSE 0 END IsReleased
, CASE WHEN ITM.CreatedDatetime <> ITM.ModifiedDateTime THEN 1 ELSE 0 END IsModified
, PSO.IsInventoryProcessingStopped
, PSO.IsSalesProcessingStopped
, PSO.IsProcurementProcessingStopped
FROM dbo.DataArea DAT
     CROSS JOIN dbo.EcoResProduct PRD
	 LEFT JOIN dbo.InventTable ITM
	   ON DAT.Id = ITM.DataAreaId 
	  AND PRD.DisplayProductNumber = ITM.ItemId
	  AND PRD.Partition = ITM.Partition
          LEFT JOIN TDM.vProductSpecificOrderSettings PSO
	        ON ITM.ItemId = PSO.ItemId 
	       AND ITM.DataAreaId = PSO.DataAreaId 
	       AND ITM.Partition = PSO.Partition
WHERE DAT.Id <> 'DAT'
   AND PRD.DisplayProductNumber = 'D0001'
ORDER BY PRD.DisplayProductNumber
, DAT.Id

Happy coding!

💫Process Management: "Invoice Capture" Process Diagram in Dynamics 365 for Finance & Operations

Introduction

Invoice Capture is a Power Apps-based application available in Dynamics 365 CRM and deeply integrated with Dynamics 365 for Finance and Operations (D365 F&O, or simply F&O). The App is designed to provide end-to-end invoice automation of Vendor invoices (see previous post for an overview). The below diagram attempts to depict the corresponding process, typically performed by the AP Clerk role, however there are also steps that are "automated" and thus performed by the System, respectively that can be performed by both actors. In addition, there are optimization and setup activities that are performed by somebody with the Administrator role. 

Invoice Capture process diagram

Disclaimer:
(1) The process diagram focuses on the main flow of data and the main exceptions. Existing and new features in Invoice Capture might change the flow of data, making the whole diagram or parts of it obsolete. Please refer to the standard documentation [1].
(2) The diagram attempts to accommodate all types of Invoices types, however I haven't tested to the full extent the Purchase Order based scenarios.
(3) Once an invoice for the same Vendor, Address and lines was processed several times, the system should be capable in time to correctly process and transfer the Invoice to F&O without AP Clerk's involvement. 

Import/Upload Invoice

The Power App listens on the configured channels (e.g. Outlook, SharePoint, OneDrive) and the incoming documents (including signature images, receipt confirmations or reminders, other attachments) are imported in the App and made available under 'Received files' page. 

Alternatively, the invoices received in hard-paper format can be scanned and be either imported manually in Invoice Capture, respectively over the configured channels. 

Troubleshoot Invoice import

The Power Automate import flows might fail to import a file if any of the documented limitations applies, for example:

• only JPG, JPEG, TIF, TIFF, PDF with a maximum of 20 MB are accepted;
• in Outlook the email landed in other folder than Inbox.

To troubleshoot this, one can try to resend the email, or import the file manually in Invoice capture/ 
Check the documentation, for a complete list of the limitations!

Capture Invoice

Once imported, the files are processed by the OCR service and moved to the ‘Captured invoices’ page if their processing is successful. The extracted metadata is used to create the Invoice record (header, lines, charges, etc.).

Void document

Files that don’t qualify as Invoices (e.g. signature images, attachments) hang in the 'Received files' page and need to be voided by the AP Clerk on a regular basis. The voided files together with duplicates of the files already processes are available in the ‘Captured invoices (Voided)’ view from where can be deleted permanently.

Troubleshoot Invoice processing

It can happen that valid files hang in ‘Received files’ with one of the following statuses:

• 'Cancelled': Use 'Retry' to restart their processing.
• 'Processing': Export/download the file manually and reprocess it, while voiding the previous entry.

The files created via non-standard tools (e.g. PDF files) can lead to incorrect metadata extraction. In other cases, special formatting might impede metadata's extraction. Upon case, one can donate the file to Microsoft and have the AI model trained by them. 

Create Master Data (D365 F&O)

When the Vendor is not available, it needs to be created in F&O from where it will be synchronized in almost real-time to the App. At minimum, it needs to be provided the Vendor Number and Name, though Vendor's creation should be done according to the general policies available in the Organization. 

Similarly for new Products, however the setup must be complete at least for the Legal entity in scope, otherwise Invoice's processing in F&O might stop. See the "Create Product" process diagram. 

The setup for new Expense types (aka Procurement categories in F&O) must follow the standard setup. One can misuse an existing Expense type and do the correction in F&O, however this might lead to further issues if the correction isn't made.

Upon case other entities might be involved (e.g. Unit of Measure4) however they should be considered as part of the general setup for Invoice Capture.

Classify Invoice 

Classifying the invoice involves identifying the Legal entity (LE), assigning the Vendor, respectively providing the Invoice type. If a similar Invoice for the same Vendor was previously processed, the values will be taken as default, though they can be modified accordingly.

A channel can be linked to a LE, and in this case the respective LE is provided as default value. Secondly, a mapping rule can be defined for the LE when a unique keyword is expected to be available in the Address. Otherwise, the AP Clerk can assign the LE manually. 
Please note that the way the permissions were set up in CRM can affect what the members of the AP Clerk can see. E.g. users that have restricted roles in CRM will see only the records associated with the LE they were assigned to. In such cases, somebody else must assign the LE to a record without a LE. 

Similarly, a mapping rule can be defined also for the Vendors when a keyword in Vendor's name is unique.

Currently, there are 3 types of Invoices: 'PO invoice', 'Header-only invoice', respectively 'Cost invoice'. The first two can be used only in combination with a PO, while a Cost invoice is used for expenses for which no PO exists. 

Start Review

Once the Invoice was correctly classified, the AP Clerk can start reviewing the Invoice record generated from the extracted metadata. 

Correct Invoice

The AP Clerk must check the recognized metadata from the Invoice header, line and Charges against the invoice, correct or confirm the values, respectively complete the missing data. The financial dimensions, the Currency, the Item, the Expense type (aka Procurement Category in F&O) and the Unit of Measure. 

Unfortunately, there are complex Invoice layouts that make it challenging for OCR to correctly extract the line-based information. It might be needed to add or remove Lines and Charges individually or completely.

Complete Review

Once the errors and warnings are handled, the AP Clerk can complete the review, however further error may appear as part of the validation routine. 

Troubleshoot Invoice issues 

Besides the mandatory fields, several constraints apply:

• The line total must match the header amount.
• The Quantity and Net amount must have the same sign. Thus, if the amount must be negative, the Quantity must be also negative.
• If not Invoice number is available, use a standard way for defining such values.

Several fields are already marked as mandatory. Consider extending the list with the attributes needed by the business. 

Transfer Invoice 

The Invoice can be transferred to F&O when no errors exist. F&O must be online for this step to be successful. 

Monitor Invoice Capture

Monitoring typically regards the whole process, though three points need special attention: (1) the import of Invoices into Invoice Capture; (2) the Invoices hanging in the 'Received files' area, respectively (3) the Invoices not transferred to F&O.

Ideally, there should be a set of reports and metrics on the CRM side to help in the process. 

Optimize Invoice Capture setup

There are several setup areas that can improve users experience while using Invoice Capture. The initial setup reflects one's knowledge about Invoice Capture, however in time optimizations can be identified especially in what concerns the mapping rules. 

Previous post <<||>> Next post

References:
[1] Microsoft Learn (2023) Invoice capture overview (link)

💫ERP Systems: Microsoft Dynamics 365's Invoice Capture (Some Thoughts to Start with)

Introduction

It's almost the year end and it's time for reviewing what went good and not that good during the year. On the "successful projects" list I can put the Invoice Capture implementation. I wrote on a previous post a short review on what the feature is about.

I had the chance of configuring Invoice Capture for Cost invoices (invoices without Purchase orders) while it was still in public preview, and we went live soon after the feature became generally available. The implementation had its challenges though in the end it was a positive experience, learning a lot from my colleagues, from Microsoft, other consultants and business users who embarked on the same journey. 

Where to Start?

Usually, it's a good idea to start with the documentation and the standard training material, which provides a good overview of what Invoice Capture is about, the steps needed for configuration, the processes involved, permissions, etc. 

You should check also the "Invoice Capture for Dynamics 365" group on Yammer (aka Viva) because besides the latest version of the Implementation Guide document are published in there also the Release notes and training videos associated with them, to which other users provide (lot of) feedback and questions. Some information is first available in the group and much later made available in the documentation. If you're facing an error or a challenge, more likely there's a conversation in there and the answer you're looking for. Otherwise, you can start a thread and the others will try to help. At least until now, Microsoft was quite active in helping.

Via FastTrack, Microsoft provided several sessions in Dec-2022 (preview) and Sep-2023 (GA) that can be used to get a good overview about the feature and its implementation. Frankly, I would start with the last session and then explore the other resources. In the process I found useful several other resources, mainly YouTube content - see Dan's Corner (link), DAFTD365 - and LinkedIn - see Hendrik M Larsen's posts, 

You might want to also check the Release planner for Finance, to see what features are in the pipeline, respectively the Ideas for Dynamics to get an idea what kind of improvements others wish for. 

In parallel, one can start sketching the "AS IS" and "TO BE" processes, and eventually put together a business case for using Invoice Capture to digitize the processing of Vendor invoices. This isn't a simple Change request, therefore it makes sense to start a project, though its scope is relatively small. 

Bridging the Gap

One can look at the "TO BE" process based on the functionality provided, respectively planned by Microsoft for Invoice capture, or look at the broader picture and sketch how an ideal digitized process should look like. If the gap between the two pictures is big, then might be a good idea to look at alternatives, which anyway should be done as part of the business case. There might be third-party tools out there (e,g, ExFlow) which provide similar functionality, however on the long term it makes sense to go with Microsoft, even if the full extent of the functionality might be not available. 

A review of other tools might be good - to understand how the ISV's approached the integration, what kind of features they provide, respectively whether the ideal digitized process makes sense. Conversely, this will imply more effort.

The current version of Invoice capture provides a good basis to build upon. One can use Power Apps or Power Automate to address some of the gaps, some gaps can be discussed with Microsoft and stress their importance, while other gaps are maybe not that important and can be dismissed. One way or another one must be ready to compromise as long as this doesn't have an important impact on the business. 

The Project

The scope of the project might be relatively small, though one should follow the best practices of Project Management and make sure that all important stakeholders are involved, that the right resources are available when needed, manage the requirements adequately, assure that the changes are adequately tested, that the users are trained, the process documented, etc.

It's important to understand that the simple configuration of Invoice capture will not be the end of the effort. As Microsoft will release further features directly and indirectly related to Invoice Capture, additional effort might be involved after the implementation went live to address the gaps, opportunities, as well as the risks. Moreover, Invoice Capture requires a learning curve; addressing the lessons learned might involve further changes in the system's setup as well in data's management. Therefore, further effort must be planned accordingly. 

Even if we talk about a full implementation or the implementation of a feature, the overall success tends to be more dependent on how the implementation is approached than on the technology involved. 

Closing Thoughts

Some of the points made here can be applied to similar feature implementations. Overall, it's important to gather enough information to start the project and in time to reach the level of depth required by it. Don't expect for things to be perfect, start small and evolve, prioritize, cover the gaps, optimize!

Previous post <<||>> Next post

💎💫SQL Reloaded: Released Products by Legal Entity in Dynamics 365 F&O

To check in which Legal Entity (LE) a Product was released using the standard UI, the user needs to go through each LE and search for the respective Product, action which can be time-consuming and error-prone if done for multiple Products. An alternative would be to use the Excel add-in or the Table Browser and export the data for each LE, respectively aggregate the data in one file and build a power pivot on top of it. If this kind of checks need to be done on a regular basis, then a better solution is to build a simple report.

When a Product is released for a Legal Entity (LE) a record is created in the InventTable table and is accessible over the dbo.EcoResReleasedProductV2Entity data entity as well. One can build the logic as a GROUP BY with an entry for each LE in scope. 

-- Released Products by Legal Entity
SELECT ItemId
, Max(CASE WHEN DataAreaId ='cnmf' THEN 1 ELSE 0 END) [cnmf]
, Max(CASE WHEN DataAreaId ='demf' THEN 1 ELSE 0 END) [demf]
, Max(CASE WHEN DataAreaId ='inmf' THEN 1 ELSE 0 END) [inmf]
, Max(CASE WHEN DataAreaId ='jpmf' THEN 1 ELSE 0 END) [jpmf]
, Max(CASE WHEN DataAreaId ='mymf' THEN 1 ELSE 0 END) [mymf]
, Max(CASE WHEN DataAreaId ='rumf' THEN 1 ELSE 0 END) [rumf]
, Max(CASE WHEN DataAreaId ='samf' THEN 1 ELSE 0 END) [samf]
, Max(CASE WHEN DataAreaId ='thmf' THEN 1 ELSE 0 END) [thmf]
, Max(CASE WHEN DataAreaId ='usmf' THEN 1 ELSE 0 END) [usmf]
, count(*) NoRecords
FROM dbo.InventTable
WHERE DataAreaId <> 'DAT'
-- AND ItemId = 'D0001'
GROUP BY ItemId
ORDER BY NoRecords DESC
-- HAVING count(*)>1 -- 

Unfortunately, the query is static and needs to be adjusted each time a new LE is added or removed. Unless the query is build and executed dynamically, there is apparently no way in SQL to include/exclude the LEs dynamically. However, one can use a cartesian product between LEs and Products, and retrieve the corresponding entry from the Released products table:

-- Legal Entities vs Products 
SELECT DAT.Id DataAreaId 
, PRD.DisplayProductNumber ItemId 
, CASE WHEN ITM.DataAreaId IS NOT NULL THEN 1 ELSE 0 END IsReleased
, CASE WHEN ITM.CreatedDatetime <> ITM.ModifiedDateTime THEN 1 ELSE 0 END IsModified
FROM dbo.DataArea DAT
     CROSS JOIN dbo.EcoResProduct PRD
	 LEFT JOIN dbo.InventTable ITM
	   ON DAT.Id = ITM.DataAreaId 
	  AND PRD.DisplayProductNumber = ITM.ItemId
	  AND PRD.Partition = ITM.Partition
WHERE DAT.Id <> 'DAT'
   AND PRD.DisplayProductNumber = 'D0001'
ORDER BY PRD.DisplayProductNumber
, DAT.Id 

Further on, the data can be aggregated in a matrix display in a paginated report, given that the respective functionality can dynamically display the LEs in scope. 

Notes:
1) The first query will run also in AX 2009, while the second will run only in D365 F&O.
2) Besides checking whether a Product was released (see IsReleased column) it's useful to check whether the Product was modified (see IsModified). If the Created and Modified timestamps are the same, then the Product was not touched after its release. 
3) The two queries can be extended to retrieve further Product-specific data (e.g. Unit of Measure, Base Prices, Default vendor, etc.).
4) It's safer to use the corresponding data entities instead of the tables.
5) It's also useful to check whether the Products are blocked for Sales, Purchasing or Inventory (see next post). 

Happy coding!