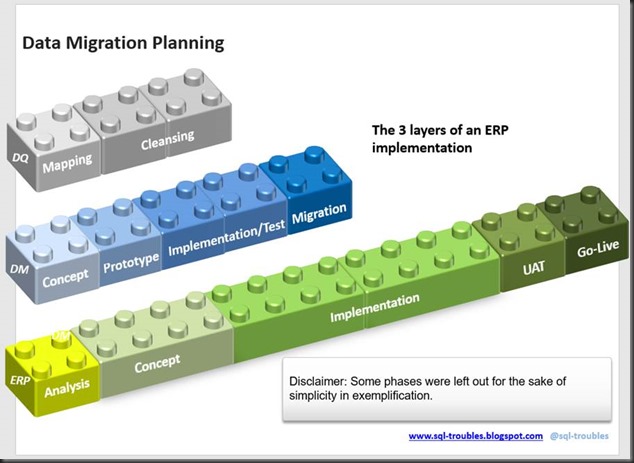
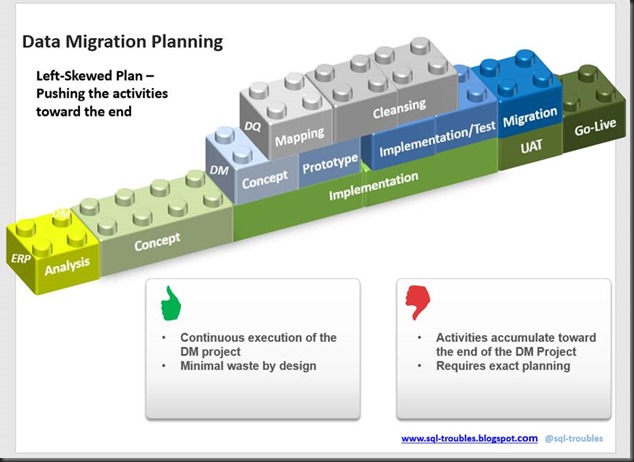
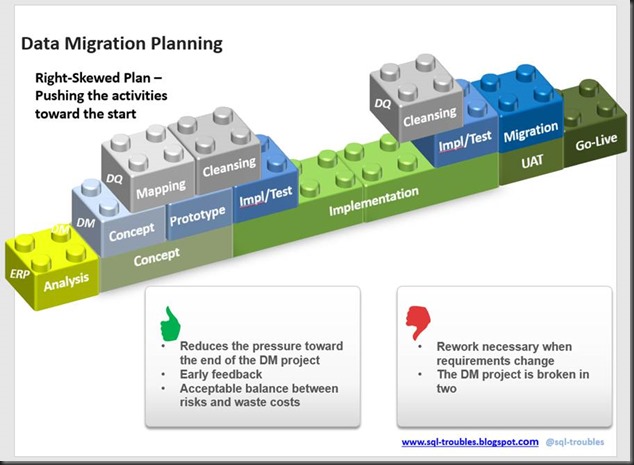
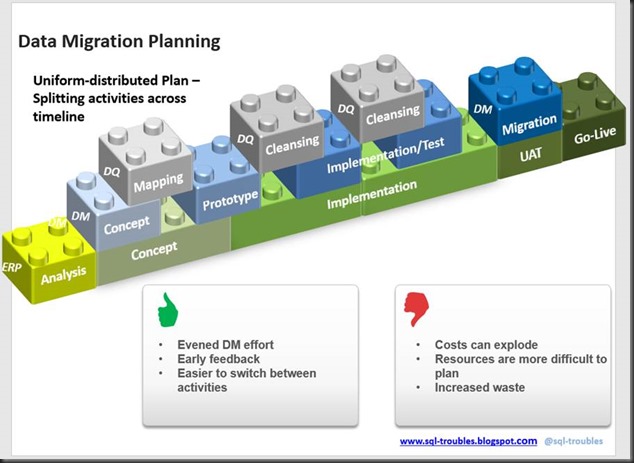
"A smaller model with fewer covariates has two advantages: it might give better predictions than a big model and it is more parsimonious (simpler). Generally, as you add more variables to a regression, the bias of the predictions decreases and the variance increases. Too few covariates yields high bias; this called underfitting. Too many covariates yields high variance; this called overfitting. Good predictions result from achieving a good balance between bias and variance. […] finding a good model involves trading of fit and complexity."
"When generating trees, it is usually optimal to grow a larger tree than is justifiable and then prune it back. The main reason this works well is that stop splitting rules do not look far enough forward. That is, stop splitting rules tend to underfit, meaning that even if a rule stops at a split for which the next candidate splits give little improvement, it may be that splitting them one layer further will give a large improvement in accuracy." (Bertrand Clarke et al, "Principles and Theory for Data Mining and Machine Learning", 2009)
"Briefly speaking, to solve a Machine Learning problem means you optimize a model to fit all the data from your training set, and then you use the model to predict the results you want. Therefore, evaluating a model need to see how well it can be used to predict the data out of the training set. Usually there are three types of the models: underfitting, fair and overfitting model [...]. If we want to predict a value, both (a) and (c) in this figure cannot work well. The underfitting model does not capture the structure of the problem at all, and we say it has high bias. The overfitting model tries to fit every sample in the training set and it did it, but we say it is of high variance. In other words, it fails to generalize new data." (Shudong Hao, "A Beginner’s Tutorial for Machine Learning Beginners", 2014)
"There are two kinds of mistakes that an inappropriate inductive bias can lead to: underfitting and overfitting. Underfitting occurs when the prediction model selected by the algorithm is too simplistic to represent the underlying relationship in the dataset between the descriptive features and the target feature. Overfitting, by contrast, occurs when the prediction model selected by the algorithm is so complex that the model fits to the dataset too closely and becomes sensitive to noise in the data."(John D Kelleher et al, "Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, and Case Studies", 2015)
"Underfitting is when a model doesn’t take into account enough information to accurately model real life. For example, if we observed only two points on an exponential curve, we would probably assert that there is a linear relationship there. But there may not be a pattern, because there are only two points to reference. [...] It seems that the best way to mitigate underfitting a model is to give it more information, but this actually can be a problem as well. More data can mean more noise and more problems. Using too much data and too complex of a model will yield something that works for that particular data set and nothing else." (Matthew Kirk, "Thoughtful Machine Learning", 2015)
"Bias is error from incorrect assumptions built into the model, such as restricting an interpolating function to be linear instead of a higher-order curve. [...] Errors of bias produce underfit models. They do not fit the training data as tightly as possible, were they allowed the freedom to do so. In popular discourse, I associate the word 'bias' with prejudice, and the correspondence is fairly apt: an apriori assumption that one group is inferior to another will result in less accurate predictions than an unbiased one. Models that perform lousy on both training and testing data are underfit." (Steven S Skiena, "The Data Science Design Manual", 2017)
"Bias occurs normally when the model is underfitted and has failed to learn enough from the training data. It is the difference between the mean of the probability distribution and the actual correct value. Hence, the accuracy of the model is different for different data sets (test and training sets). To reduce the bias error, data scientists repeat the model-building process by resampling the data to obtain better prediction values." (Umesh R Hodeghatta & Umesha Nayak, "Business Analytics Using R: A Practical Approach", 2017)
"High-bias models typically produce simpler models that do not overfit and in those cases the danger is that of underfitting. Models with low-bias are typically more complex and that complexity enables us to represent the training data in a more accurate way. The danger here is that the flexibility provided by higher complexity may end up representing not only a relationship in the data but also the noise. Another way of portraying the bias-variance trade-off is in terms of complexity v simplicity." (Jesús Rogel-Salazar, "Data Science and Analytics with Python", 2017)
"If either bias or variance is high, the model can be very far off from reality. In general, there is a trade-off between bias and variance. The goal of any machine-learning algorithm is to achieve low bias and low variance such that it gives good prediction performance. In reality, because of so many other hidden parameters in the model, it is hard to calculate the real bias and variance error. Nevertheless, the bias and variance provide a measure to understand the behavior of the machine-learning algorithm so that the model model can be adjusted to provide good prediction performance." (Umesh R Hodeghatta & Umesha Nayak, "Business Analytics Using R: A Practical Approach", 2017)
"Overfitting and underfitting are two important factors that could impact the performance of machine-learning models. Overfitting occurs when the model performs well with training data and poorly with test data. Underfitting occurs when the model is so simple that it performs poorly with both training and test data. [...] When the model does not capture and fit the data, it results in poor performance. We call this underfitting. Underfitting is the result of a poor model that typically does not perform well for any data." (Umesh R Hodeghatta & Umesha Nayak, "Business Analytics Using R: A Practical Approach", 2017)
"Overfitting refers to the phenomenon where a model is highly fitted on a dataset. This generalization thus deprives the model from making highly accurate predictions about unseen data. [...] Underfitting is a phenomenon where the model is not trained with high precision on data at hand. The treatment of underfitting is subject to bias and variance. A model will have a high bias if both train and test errors are high [...] If a model has a high bias type underfitting, then the remedy can be to increase the model complexity, and if a model is suffering from high variance type underfitting, then the cure can be to bring in more data or otherwise make the model less complex." (Danish Haroon, "Python Machine Learning Case Studies", 2017)
"The tension between bias and variance, simplicity and complexity, or underfitting and overfitting is an area in the data science and analytics process that can be closer to a craft than a fixed rule. The main challenge is that not only is each dataset different, but also there are data points that we have not yet seen at the moment of constructing the model. Instead, we are interested in building a strategy that enables us to tell something about data from the sample used in building the model." (Jesús Rogel-Salazar, "Data Science and Analytics with Python", 2017)
"Even though a natural way of avoiding overfitting is to simply build smaller networks (with fewer units and parameters), it has often been observed that it is better to build large networks and then regularize them in order to avoid overfitting. This is because large networks retain the option of building a more complex model if it is truly warranted. At the same time, the regularization process can smooth out the random artifacts that are not supported by sufficient data. By using this approach, we are giving the model the choice to decide what complexity it needs, rather than making a rigid decision for the model up front (which might even underfit the data)." (Charu C Aggarwal, "Neural Networks and Deep Learning: A Textbook", 2018)
"One of the most common problems that you will encounter when training deep neural networks will be overfitting. What can happen is that your network may, owing to its flexibility, learn patterns that are due to noise, errors, or simply wrong data. [...] The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e., the noise) as if that variation represented the underlying model structure. The opposite is called underfitting - when the model cannot capture the structure of the data." (Umberto Michelucci, "Applied Deep Learning: A Case-Based Approach to Understanding Deep Neural Networks", 2018)
"The high generalization error in a neural network may be caused by several reasons. First, the data itself might have a lot of noise, in which case there is little one can do in order to improve accuracy. Second, neural networks are hard to train, and the large error might be caused by the poor convergence behavior of the algorithm. The error might also be caused by high bias, which is referred to as underfitting. Finally, overfitting (i.e., high variance) may cause a large part of the generalization error. In most cases, the error is a combination of more than one of these different factors." (Charu C Aggarwal, "Neural Networks and Deep Learning: A Textbook", 2018)
"The trick is to walk the line between underfitting and overfitting. An underfit model has low variance, generally making the same predictions every time, but with extremely high bias, because the model deviates from the correct answer by a significant amount. Underfitting is symptomatic of not having enough data points, or not training a complex enough model. An overfit model, on the other hand, has memorized the training data and is completely accurate on data it has seen before, but varies widely on unseen data. Neither an overfit nor underfit model is generalizable - that is, able to make meaningful predictions on unseen data." (Benjamin Bengfort et al, "Applied Text Analysis with Python: Enabling Language-Aware Data Products with Machine Learning", 2018)
"Any fool can fit a statistical model, given the data and some software. The real challenge is to decide whether it actually fits the data adequately. It might be the best that can be obtained, but still not good enough to use." (Robert Grant, "Data Visualization: Charts, Maps and Interactive Graphics", 2019)