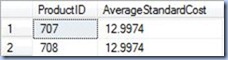
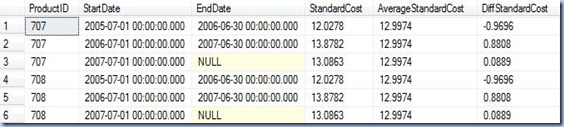
"For a curve the vertical scale. whenever practicable, should be so selected that the zero line will appear on the diagram. [...] If the zero line of the vertical scale will not normally appear on the curve diagram, the zero line should be shown by the use of a horizontal break in the diagram." (Joint Committee on Standards for Graphic Presentation, "Publications of the American Statistical Association" Vol.14 (112), 1915)
"If only one scale is used, it should be placed at the left-hand side of the chart. In very large charts it is sometimes desirable to repeat the scale at the right-hand side as well. Where two different units of measurement are used in the scales, the units should be carefully named so that there will be no danger of the reader's using the right-hand and the left-hand scales interchangeably as though they represented the same unit." (Willard C Brinton, "Graphic Methods for Presenting Facts", 1919)
"It should be a strict rule for all kinds of curve plotting that the horizontal scale must be used. for the independent variable and the vertical scale for the dependent variable. When the curves are plotted by this rule the reader can instantly select a set of conditions from the horizontal scale and read the information from the vertical scale. If there were no rule relating to the arrangement of scales for the independent and dependent variables, the reader would never be able to tell whether he should approach a chart from the vertical scale and read the information from the horizontal scale, or the reverse." (Willard C Brinton, "Graphic Methods for Presenting Facts", 1919)
"Sometimes the scales of these accompanying charts are so large that the reader is puzzled to get clearly in his mind what the whole chart is driving at. There is a possibility of making a simple chart on such a large scale that the mere size of the chart adds to its complexity by causing the reader to glance from one side of the chart to the other in trying to get a condensed visualization of the chart." (Willard C Brinton, "Graphic Methods for Presenting Facts", 1919)
"The scales of any curve-chart should be so selected that the chart will not be exaggerated in either the horizontal or the vertical direction. It is possible to cause a visual exaggeration of data by carelessly or intentionally selecting a scale which unduly stretches the chart in either the horizontal or the vertical direction. Just as the English language can be used to exaggerate to the ear, so charts can exaggerate to the eye." (Willard C Brinton, "Graphic Methods for Presenting Facts", 1919)
"The zero of the scale should appear on every chart, and should shown by a heavy line carried across the sheet. If this is not done the reader may assume the bottom of the sheet to be zero and so be mis- led. The scale should be graduated from zero to a little over the maximum figure to be plotted on the charts, so that there will be a space between the highest peak on the curve and the top of the chart." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"Under certain conditions, however, the ordinary form of graphic chart is slightly misleading. It will be conceded that its true function is to portray comparative fluctuations. This result is practically secured when the factors or quantities compared are nearly of the same value or volume, but analysis will show that this is not accomplished when the amounts compared differ greatly in value or volume. [...] The same criticism applies to charts which employ or more scales for various curve. If the different scale are in proper proportion, the result is the same as with one scale, but when two or more scales are used which are not proportional an indication may be given with respect to comparative fluctuations which is absolutely false." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"When dealing with very large quantities it is not always practicable to use a scale which starts at zero, and is carried up by even steps to a figure representing the highest peak on the curve. Such a chart would either be too large for convenient handling, or else the scale would have to be condensed so that only very large fluctuations would be indicated on the curve. In a ease of this kind the best practice is to start the at zero, and just above this point draw a wavy line across the sheet to indicate that the scale is broken at this point. This line can be very easily drawn with an ordinary serrated edge ruler as used by many accountants. The scale starts again on the upper side of the wavy line at a figure a little lower than the lowest point on the curve, and is carried up by even steps to a figure a little above the highest point to be shown on the curve." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"With the ordinary scale, fluctuations in large factors are very noticeable, while relatively greater fluctuations in smaller factors are barely apparent. The semi-logarithmic scale permits the graphic representation of changes in every quantity on the same basis, without respect to the magnitude of the quantity itself. At the same time, it shows the actual value by reference to the numbers in the scale column. By indicating both absolute and relative value and changes to one scale, it combines the advantages of both the natural and percentage scale, without the disadvantages of either." (Allan C Haskell, "How to Make and Use Graphic Charts", 1919)
"Admittedly a chart is primarily a picture, and for presentation purposes should be treated as such; but in most charts it is desirable to be able to read the approximate magnitudes by reference to the scales. Such reference is almost out of the question without some rulings to guide the eye. Second, the picture itself may be misleading without enough rulings to keep the eye 'honest'. Although sight is the most reliable of our senses for measuring (and most other) purposes, the unaided eye is easily deceived; and there are numerous optical illusions to prove it. A third reason, not vital, but still of some importance, is that charts without rulings may appear weak and empty and may lack the structural unity desirable in any illustration." (Kenneth W Haemer, "Hold That Line. A Plea for the Preservation of Chart Scale Ruling", The American Statistician Vol. 1 (1) 1947)
"[….] double-scale charts are likely to be misleading unless the two zero values coincide (either on or off the chart). To insure an accurate comparison of growth the scale intervals should be so chosen that both curves meet at some point. This treatment produces the effect of percentage relatives or simple index numbers with the point of juncture serving as the base point. The principal advantage of this form of presentation is that it is a short-cut method of comparing the relative change of two or more series without computation. It is especially useful for bringing together series that either vary widely in magnitude or are measured in different units and hence cannot be compared conveniently on a chart having only one absolute-amount scale. In general, the double scale treatment should not be used for presenting growth comparisons to the general reader." (Kenneth W Haemer, "Double Scales Are Dangerous", The American Statistician Vol. 2 (3) , 1948)
"[…] many readers are confused by the presence of two scales, and either use the wrong one or simply disregard both. Also, the general reader has the disconcerting habit of believing that because one curve is higher than another, it is also larger in magnitude. This leads to all sorts of misconceptions." (Kenneth W Haemer, "Double Scales Are Dangerous", The American Statistician Vol. 2 (3) , 1948)
"The ratio chart not only correctly represents relative changes but also indicates absolute amounts at the same time. Because of its distinctive structure, it is referred to as a semilogarithmic chart. The vertical axis is ruled logarithmically and the horizontal axis arithmetically. The continued narrowing of the spacings of the scale divisions on the vertical axis is characteristic of logarithmic rulings; the equal intervals on the horizontal axis are indicative of arithmetic rulings." (Anna C Rogers, "Graphic Charts Handbook", 1961)
"Logging size transforms the original skewed distribution into a more symmetrical one by pulling in the long right tail of the distribution toward the mean. The short left tail is, in addition, stretched. The shift toward symmetrical distribution produced by the log transform is not, of course, merely for convenience. Symmetrical distributions, especially those that resemble the normal distribution, fulfill statistical assumptions that form the basis of statistical significance testing in the regression model." (Edward R Tufte, "Data Analysis for Politics and Policy", 1974)
"Logging skewed variables also helps to reveal the patterns in the data. […] the rescaling of the variables by taking logarithms reduces the nonlinearity in the relationship and removes much of the clutter resulting from the skewed distributions on both variables; in short, the transformation helps clarify the relationship between the two variables. It also […] leads to a theoretically meaningful regression coefficient." (Edward R Tufte, "Data Analysis for Politics and Policy", 1974)
"The logarithmic transformation serves several purposes: (1) The resulting regression coefficients sometimes have a more useful theoretical interpretation compared to a regression based on unlogged variables. (2) Badly skewed distributions - in which many of the observations are clustered together combined with a few outlying values on the scale of measurement - are transformed by taking the logarithm of the measurements so that the clustered values are spread out and the large values pulled in more toward the middle of the distribution. (3) Some of the assumptions underlying the regression model and the associated significance tests are better met when the logarithm of the measured variables is taken." (Edward R Tufte, "Data Analysis for Politics and Policy", 1974)
"The scales used are important; contracting or expanding the vertical or horizontal scales will change the visual picture. The trend lines need enough grid lines to obviate difficulty in reading the results properly. One must be careful in the use of cross-hatching and shading, both of which can create illusions. Horizontal rulings tend to reduce the appearance. while vertical lines enlarge it. In summary, graphs must be reliable, and reliability depends not only on what is presented but also on how it is presented." (Anker V Andersen, "Graphing Financial Information: How accountants can use graphs to communicate", 1983)
"The time-series plot is the most frequently used form of graphic design. With one dimension marching along to the regular rhythm of seconds, minutes, hours, days, weeks, months, years, centuries, or millennia, the natural ordering of the time scale gives this design a strength and efficiency of interpretation found in no other graphic arrangement." (Edward R Tufte, "The Visual Display of Quantitative Information", 1983)
"It is common for positive data to be skewed to the right: some values bunch together at the low end of the scale and others trail off to the high end with increasing gaps between the values as they get higher. Such data can cause severe resolution problems on graphs, and the common remedy is to take logarithms. Indeed, it is the frequent success of this remedy that partly accounts for the large use of logarithms in graphical data display." (William S Cleveland, "The Elements of Graphing Data", 1985)
"When magnitudes are graphed on a logarithmic scale, percents and factors are easier to judge since equal multiplicative factors and percents result in equal distances throughout the entire scale." (William S Cleveland, "The Elements of Graphing Data", 1985)
"When the data are magnitudes, it is helpful to have zero included in the scale so we can see its value relative to the value of the data. But the need for zero is not so compelling that we should allow its inclusion to ruin the resolution of the data on the graph." (William S Cleveland, "The Elements of Graphing Data", 1985)
"The logarithm is one of many transformations that we can apply to univariate measurements. The square root is another. Transformation is a critical tool for visualization or for any other mode of data analysis because it can substantially simplify the structure of a set of data. For example, transformation can remove skewness toward large values, and it can remove monotone increasing spread. And often, it is the logarithm that achieves this removal." (William S Cleveland, "Visualizing Data", 1993)
"The rule is that a graph of a change in a variable with time should always have a vertical scale that starts with zero. Otherwise, it is inherently misleading." (Douglas A Downing & Jeffrey Clark, "Forgotten Statistics: A Self-Teaching Refresher Course", 1996)
"The more clues to meaning that are supplied
elsewhere, the less the need for cluttersome scales." (Eric Meyer, "Designing
Infographics", 1997)
"Choose scales wisely, as they have a profound influence on the interpretation of graphs. Not all scales require that zero be included, but bar graphs and other graphs where area is judged do require it." (Naomi B Robbins, "Creating More effective Graphs", 2005)
"The visual representation of a scale - an axis with ticks - looks like a ladder. Scales are the types of functions we use to map varsets to dimensions. At first glance, it would seem that constructing a scale is simply a matter of selecting a range for our numbers and intervals to mark ticks. There is more involved, however. Scales measure the contents of a frame. They determine how we perceive the size, shape, and location of graphics. Choosing a scale (even a default decimal interval scale) requires us to think about what we are measuring and the meaning of our measurements. Ultimately, that choice determines how we interpret a graphic." (Leland Wilkinson, "The Grammar of Graphics" 2nd Ed., 2005)
"Use a logarithmic scale when it is important to understand percent change or multiplicative factors. […] Showing data on a logarithmic scale can cure skewness toward large values." (Naomi B Robbins, "Creating More effective Graphs", 2005)
"Use a scale break only when necessary. If a break cannot be avoided, use a full scale break. Taking logs can cure the need for a break." (Naomi B Robbins, "Creating More effective Graphs", 2005)
"It is important to pay heed to the following detail: a disadvantage of logarithmic diagrams is that a graphical integration is not possible, i.e., the area under the curve (the integral) is of no relevance." (Manfred Drosg, "Dealing with Uncertainties: A Guide to Error Analysis", 2007)
"Another way to obscure the truth is to hide it with relative numbers. […] Relative scales are always given as percentages or proportions. An increase or decrease of a given percentage only tells us part of the story, however. We are missing the anchoring of absolute values." (Brian Suda, "A Practical Guide to Designing with Data", 2010)
"One way a chart can lie is through overemphasis of the size and scale of items, particularly when the dimension of depth isnʼt considered." (Brian Suda, "A Practical Guide to Designing with Data", 2010)
"Color can tell us where to look, what to compare and contrast, and it can give us a visual scale of measure. Because color can be so effective, it is often used for multiple purposes in the same graphic - which can create graphics that are dazzling but difficult to interpret. Separating the roles that color can play makes it easier to apply color specifically for encouraging different kinds of visual thinking. [...] Choose colors to draw attention, to label, to show relationships (compare and contrast), or to indicate a visual scale of measure." (Felice C Frankel & Angela H DePace, "Visual Strategies", 2012)
"Geographic maps have the advantage of being true to scale - great for walking. Diagrams have the advantage of being easily imaged and remembered, often true to a non-pedestrian experience, and the ability to open up congestion, reduce empty space, and use real estate efficiently. Hybrids 'mapograms' ? - often have the disadvantages of both map and diagram with none of the corresponding advantages." (Joel Katz, "Designing Information: Human factors and common sense in information design", 2012)
"Context (information that lends to better understanding the who, what, when, where, and why of your data) can make the data clearer for readers and point them in the right direction. At the least, it can remind you what a graph is about when you come back to it a few months later. […] Context helps readers relate to and understand the data in a visualization better. It provides a sense of scale and strengthens the connection between abstract geometry and colors to the real world." (Nathan Yau, "Data Points: Visualization That Means Something", 2013)
"Whichever scale is used to represent the data, it is important to keep it consistent in data presentations. The principles of clarity, precision, and efficiency are rarely met if the measurement scales change within tables." (John Hoffmann, "Principles of Data Management and Presentation", 2017)